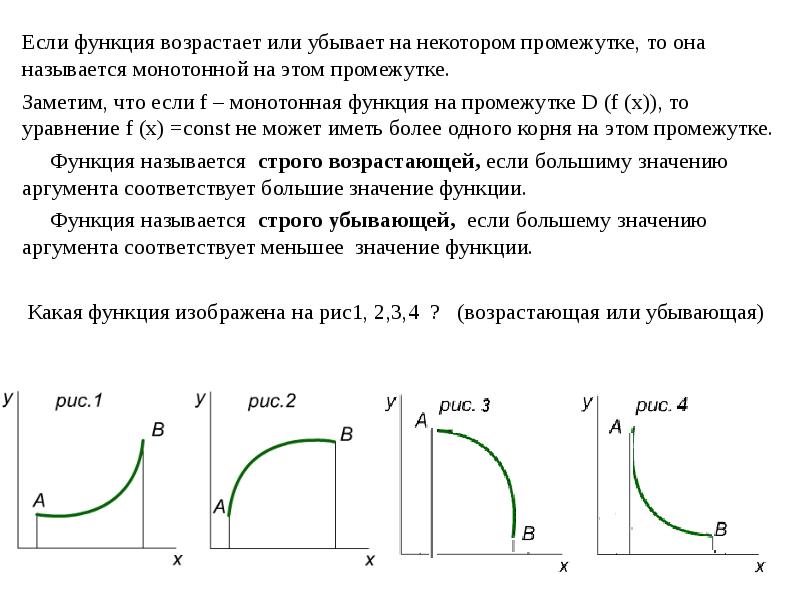
Понимание свойств функции: когда она возрастает и убывает
Эта страница посвящена пониманию того, как определить, возрастает ли функция или убывает. Узнайте, как анализировать функции и находить их поведение на разных интервалах.

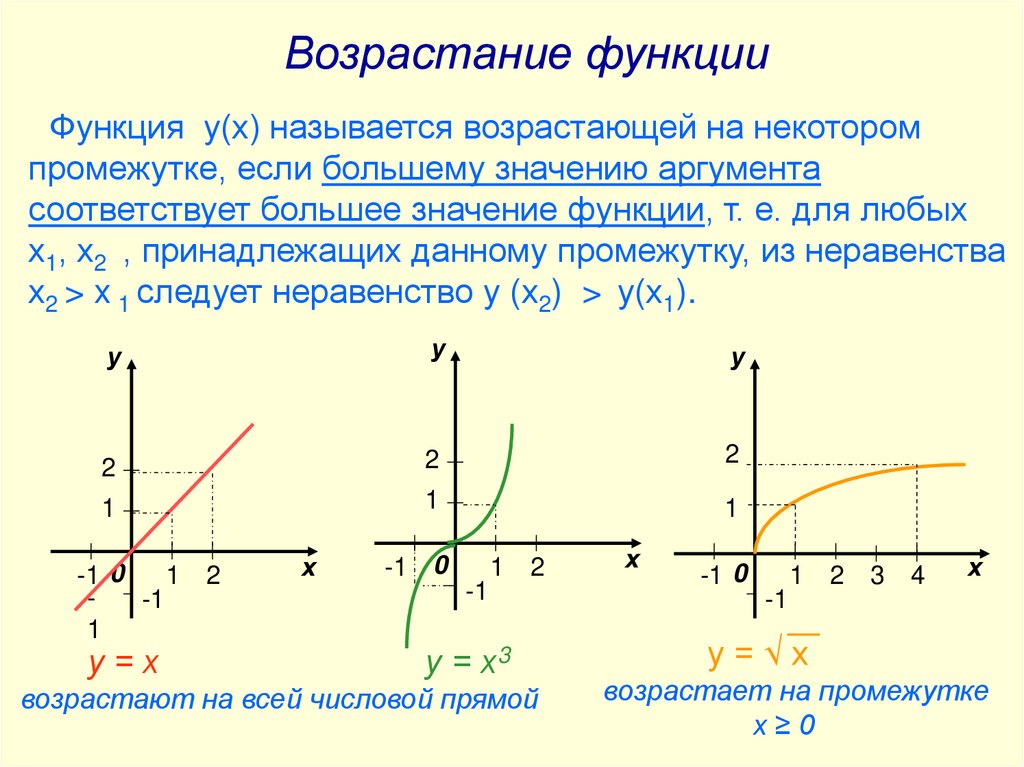
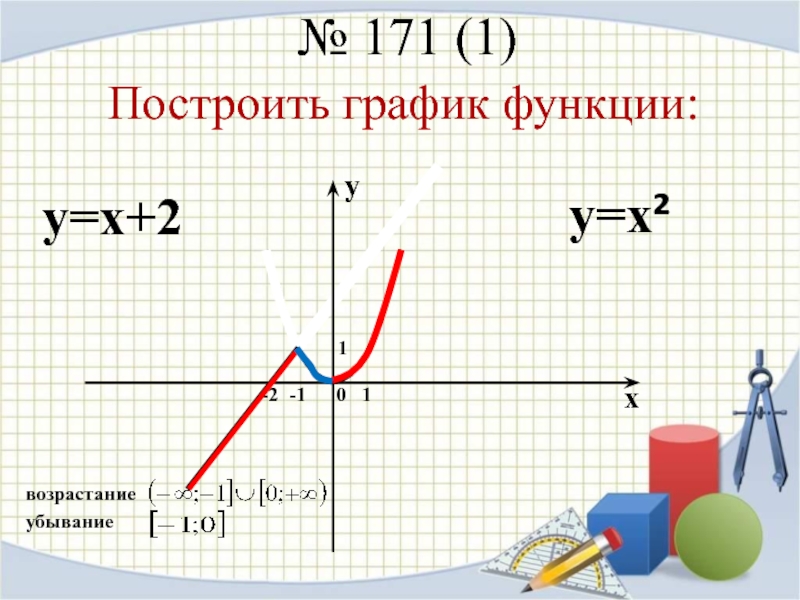
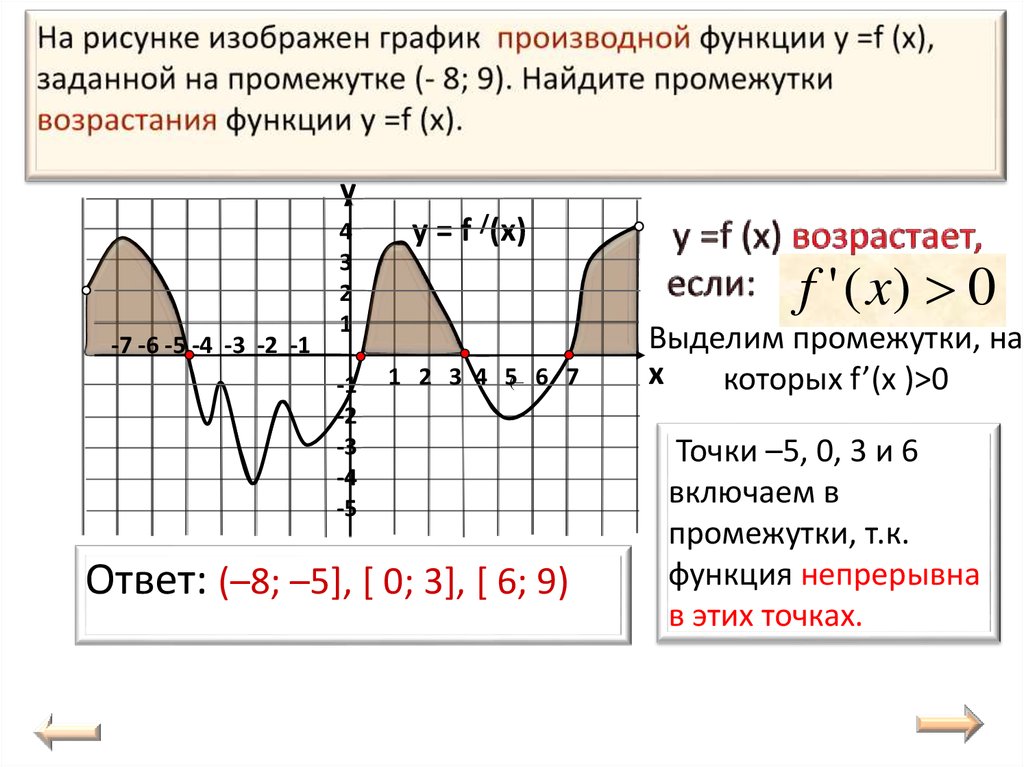
Изучите производную функции, чтобы понять её поведение. Если производная положительна, функция возрастает; если отрицательна, функция убывает.
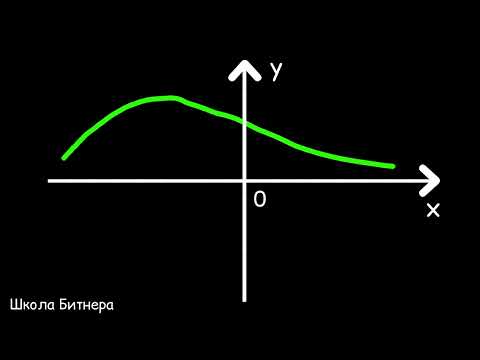
Убывает, возрастает, положительна, отрицательна

Для функций, заданных графически, определите интервалы, где график поднимается или опускается. Это поможет визуально понять, где функция возрастает или убывает.
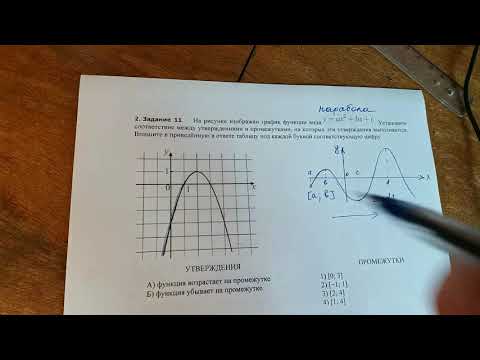
ОГЭ, математика, №11 Графики функций, возрастание и убывание
Используйте таблицы знаков производной для систематического анализа, где функция возрастает и где убывает.

Задание 11 Графики функций ОГЭ по математике 2024 Умскул
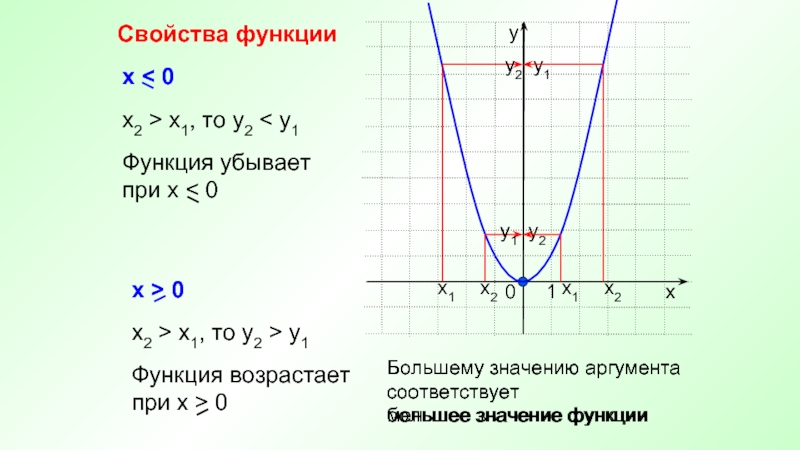

Проверьте точки максимума и минимума функции, так как изменения в их поведении могут указывать на точки перехода от возрастания к убыванию и наоборот.
Возрастание функции - убывание функции - 9 класс Макарычев
При работе с многочленами разложите их на множители и исследуйте поведение каждого множителя по отдельности.
Свойства функции. Промежутки возрастания и убывания функции. 10 класс.
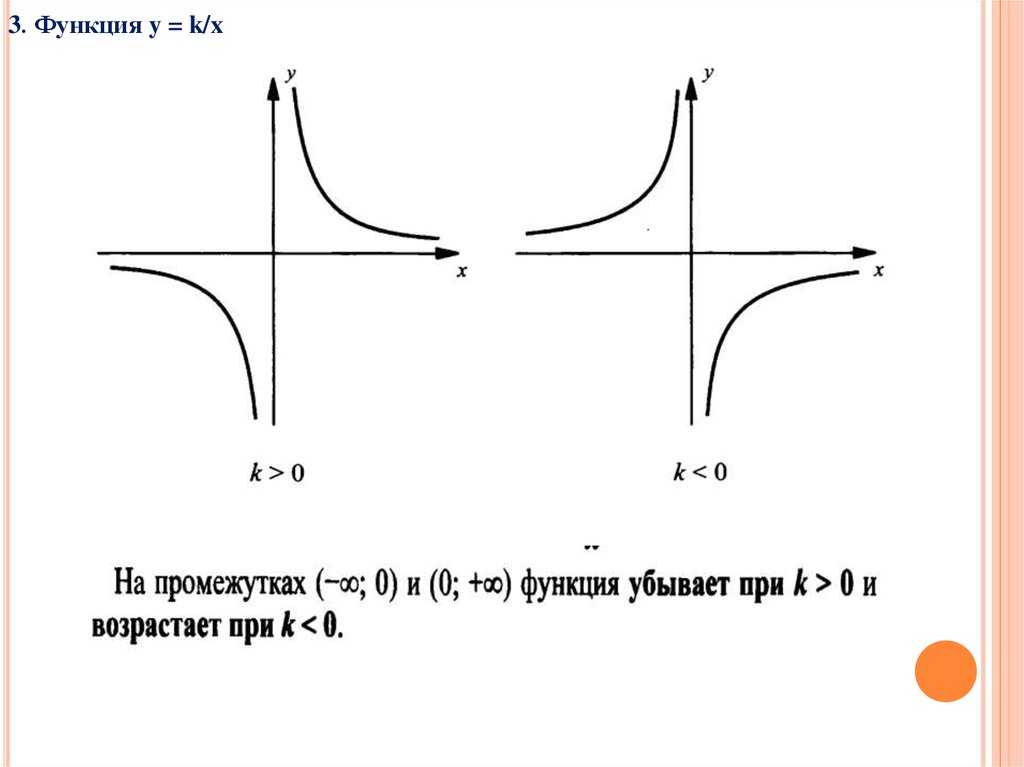
Для дробных функций проверьте знаки числителя и знаменателя, чтобы определить, как функция ведет себя в разных областях.
Используйте вычислительные инструменты и графические калькуляторы для упрощения анализа функций и более точного определения интервалов возрастания и убывания.

Промежутки возрастания и убывания функции. 10 класс.
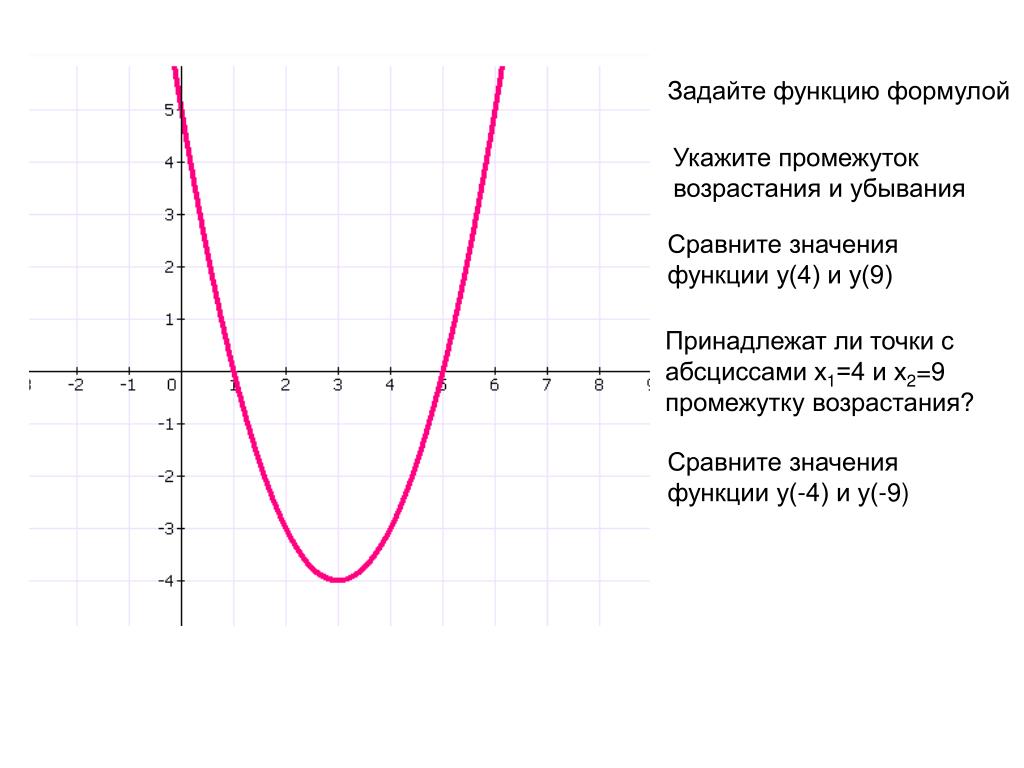
При анализе сложных функций с несколькими переменными исследуйте частные производные для понимания, как функция изменяется по каждой переменной.
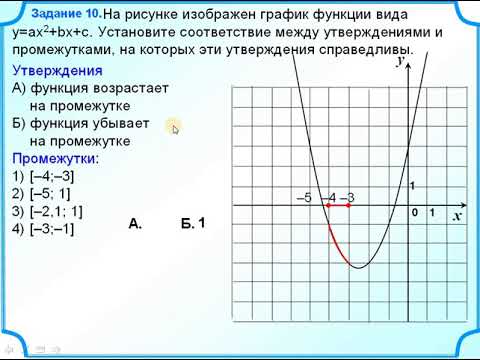
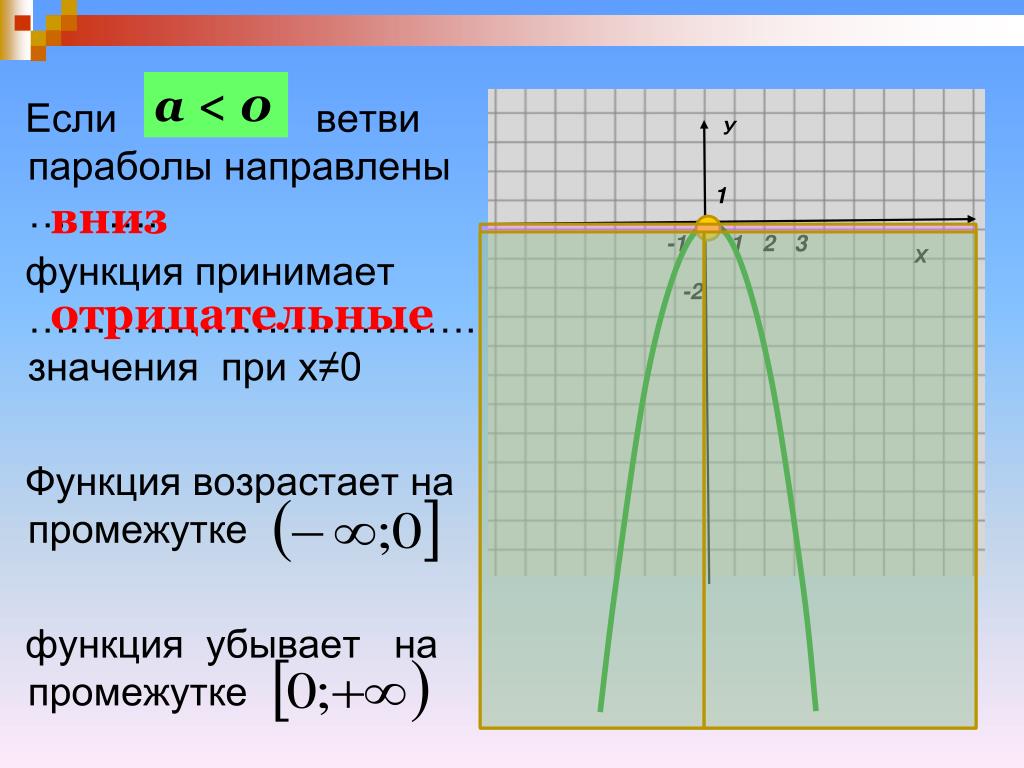
Задание 10 Квадратичная функция Промежутки возрастания убывания
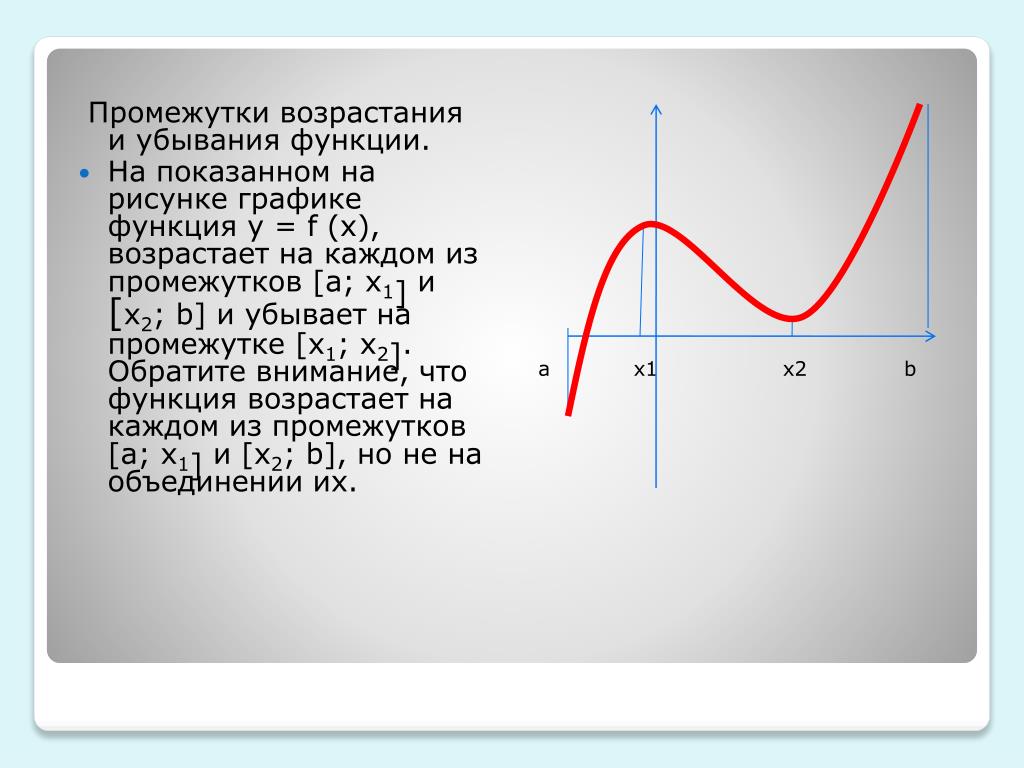
Обратите внимание на асимптоты функции, так как они могут указывать на поведение функции в пределах больших или малых значений переменных.

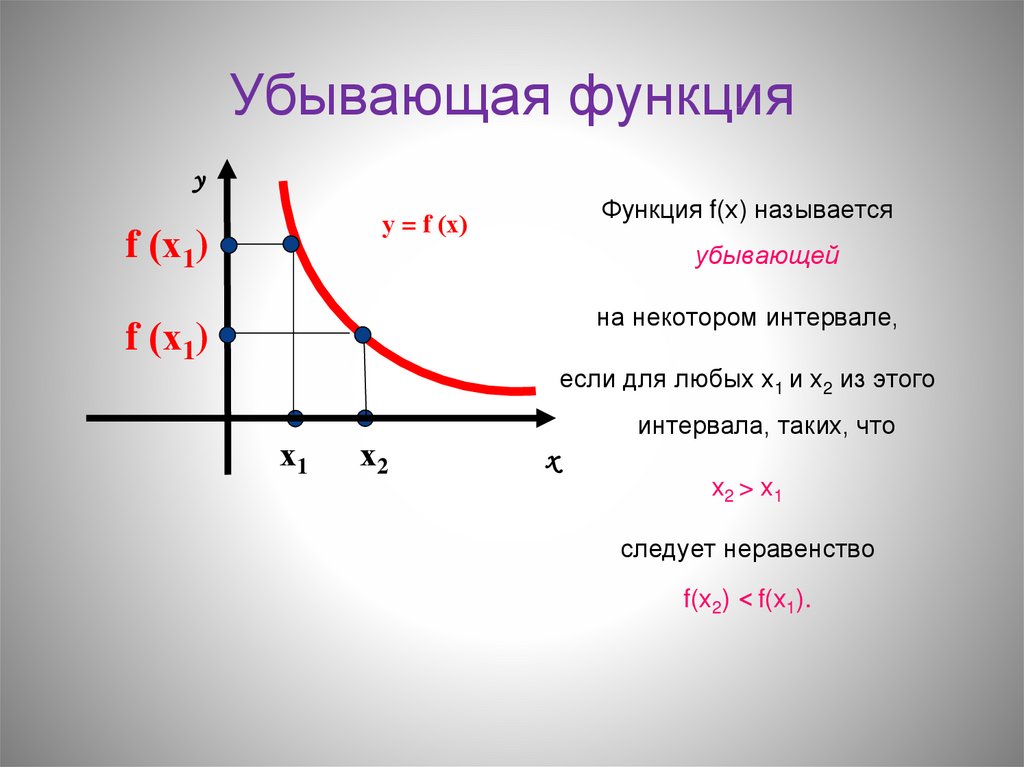
Как доказать, что функция убывает или возрастает
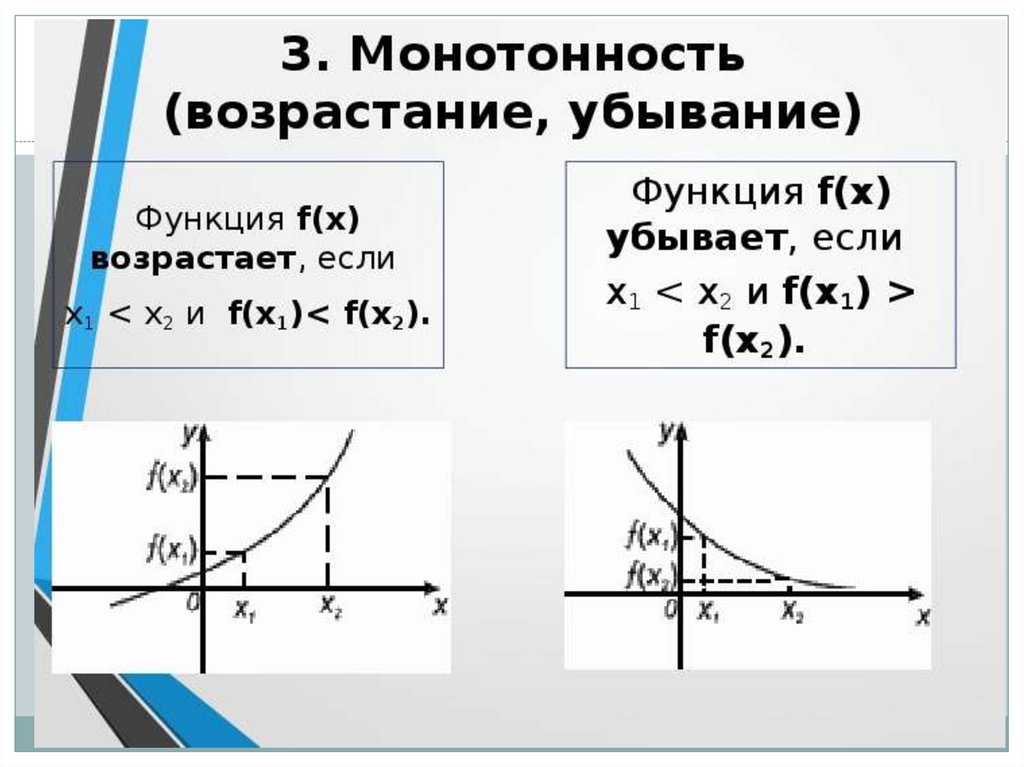
При решении задач с функциями, обращайте внимание на контекст задачи, так как это может влиять на интерпретацию поведения функции.