Определение и использование угла в параллелограмме, равного 30 градусам
В этой статье мы рассмотрим, как найти и использовать угол в параллелограмме, который равен 30 градусам. Мы предоставим полезные советы и рекомендации для работы с геометрией параллелограммов, которые помогут вам лучше понять эту тему и применять знания на практике.


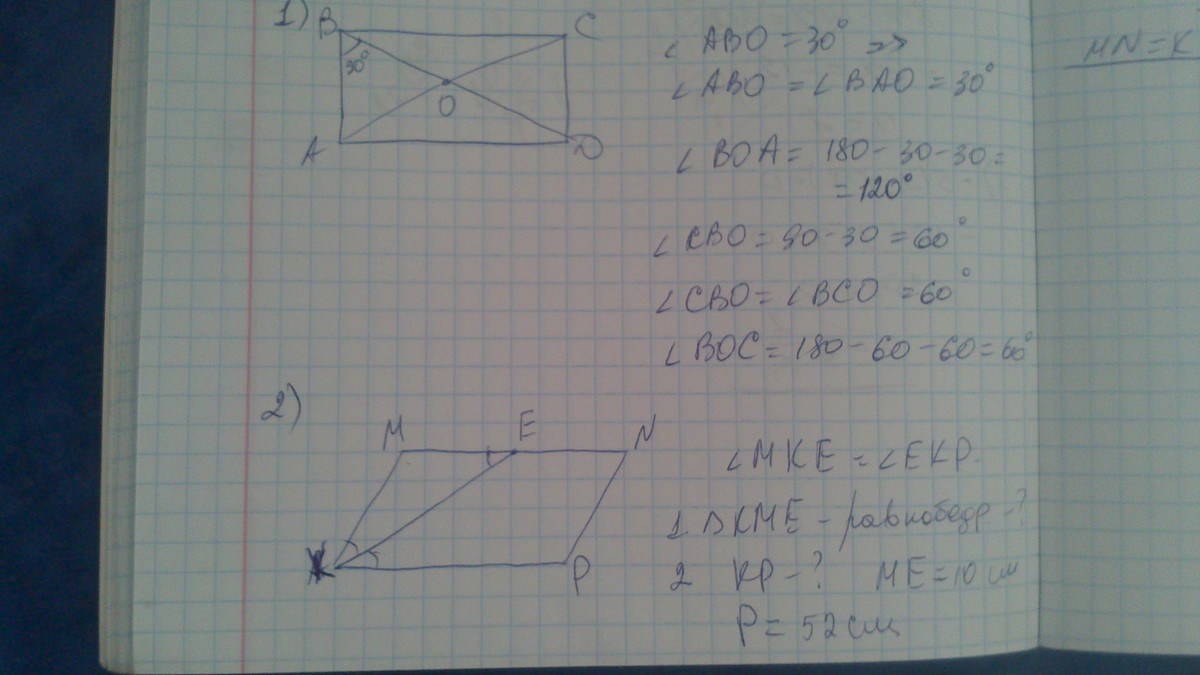
При работе с параллелограммом, у которого один из углов равен 30 градусам, помните, что сумма углов в любом параллелограмме составляет 360 градусов.

Угол 30 градусов без угломера

Если один угол параллелограмма равен 30 градусам, то противоположный угол также будет равен 30 градусам, а два оставшихся угла будут равны 150 градусам.

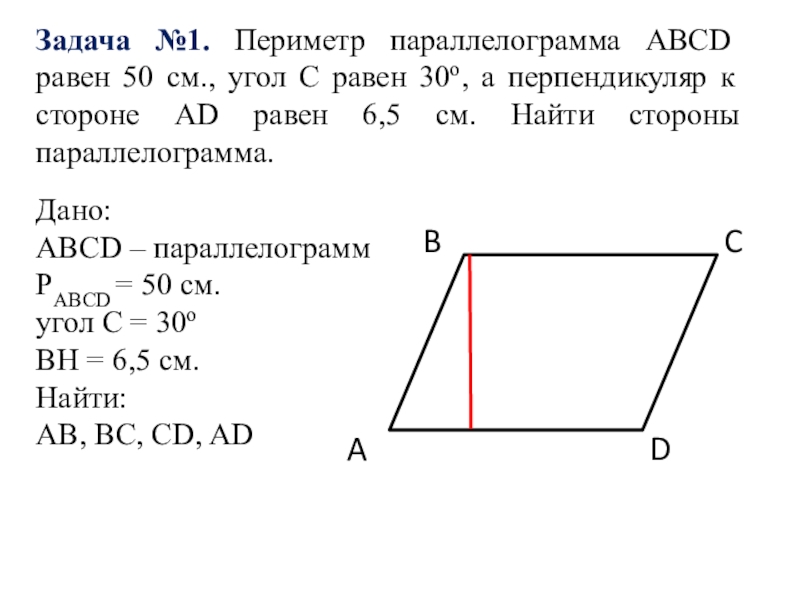
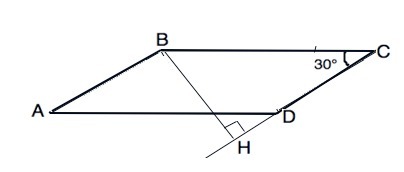
№373. Периметр параллелограмма ABCD равен 50 см, ∠C = 30°, а перпендикуляр ВН
Используйте свойства параллелограммов для вычисления других углов и сторон, если один из углов равен 30 градусам.

Построить угол 30°


Не забывайте, что противоположные стороны параллелограмма равны, что может упростить вычисления при работе с углами.

Г: Найдите стороны параллелограмма, периметр которого равен 60 см, острый угол 30 градусов

Чтобы найти длину диагоналей параллелограмма, можно использовать косинус угла, равного 30 градусам, в соответствующих формулах.

Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // Геометрия

При построении параллелограмма с углом 30 градусов, убедитесь, что соблюдаются все свойства фигуры для точного выполнения чертежа.
7 кл г. Теорема: «катет лежавший напротив угла в 30 градусов равен половине гипотенузы»
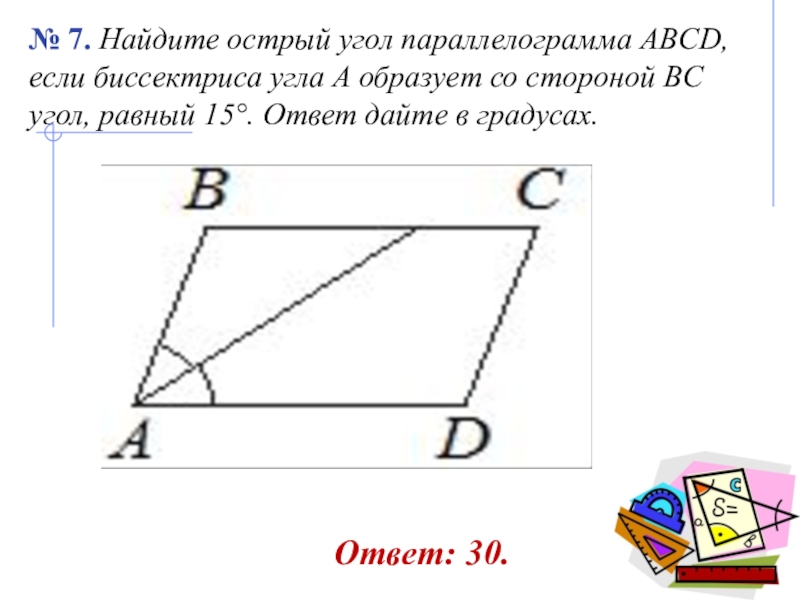
Для проверки правильности расчетов углов используйте геометрические программы или калькуляторы, чтобы избежать ошибок.

№461. Смежные стороны параллелограмма равны 12 см и 14 см, а его острый угол равен 30°. Найдите
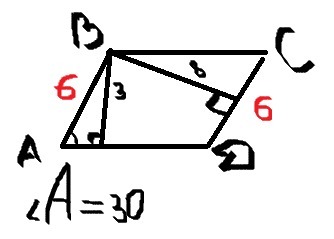
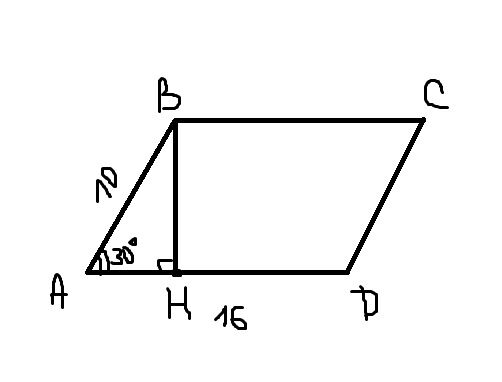
Рассмотрите возможность использования треугольников, образующихся в параллелограмме, для упрощения задач по нахождению углов и сторон.
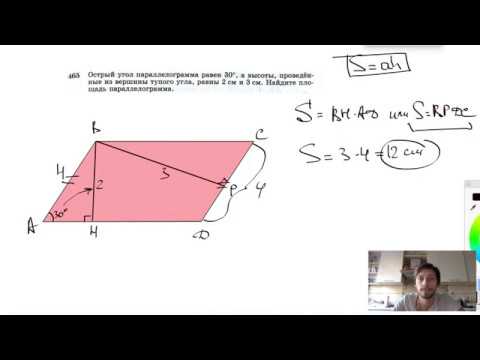
№465. Острый угол параллелограмма равен 30°, а высоты, проведенные из вершины тупого угла, равны


Используйте свойства параллелограммов для решения задач, связанных с нахождением площади, зная угол в 30 градусов.
Практикуйтесь в решении задач с параллелограммами разных типов, чтобы лучше понять влияние углов на свойства фигуры.