Теория автоматов: важнейший раздел дискретной математики
Теория автоматов является ключевым разделом дискретной математики, изучающим математические модели вычислительных устройств. На этой странице представлены фотографии и полезные советы для изучения данной темы.
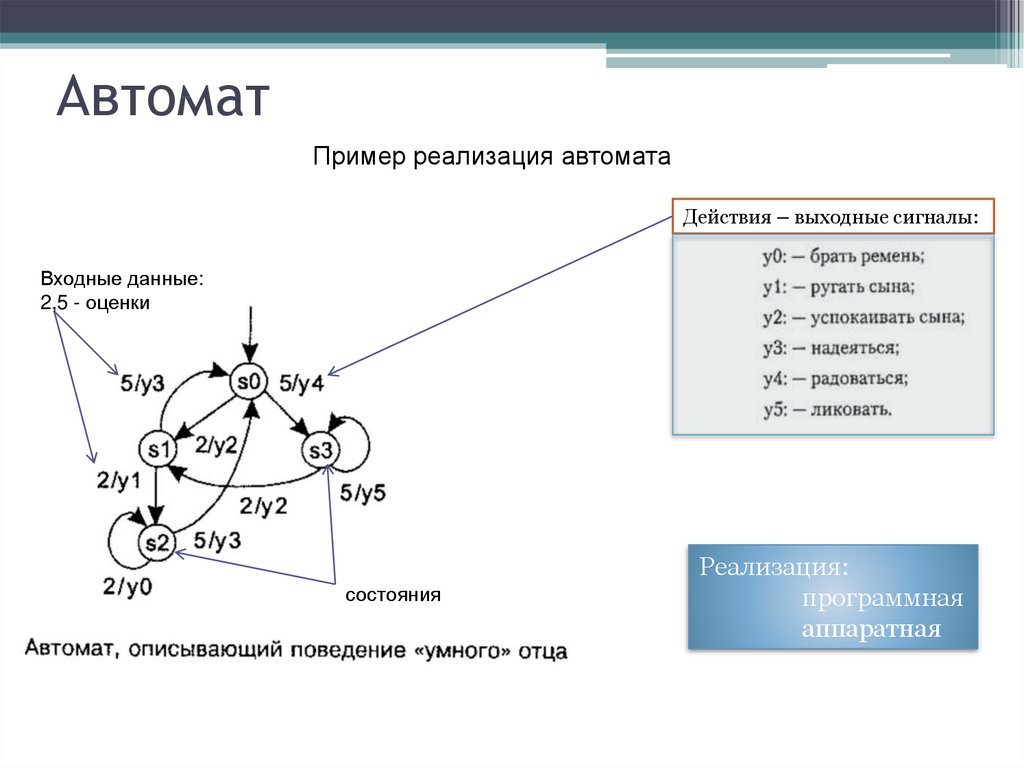

Начните с изучения основных понятий теории автоматов, таких как детерминированные и недетерминированные конечные автоматы.

Как построить автомат по функции
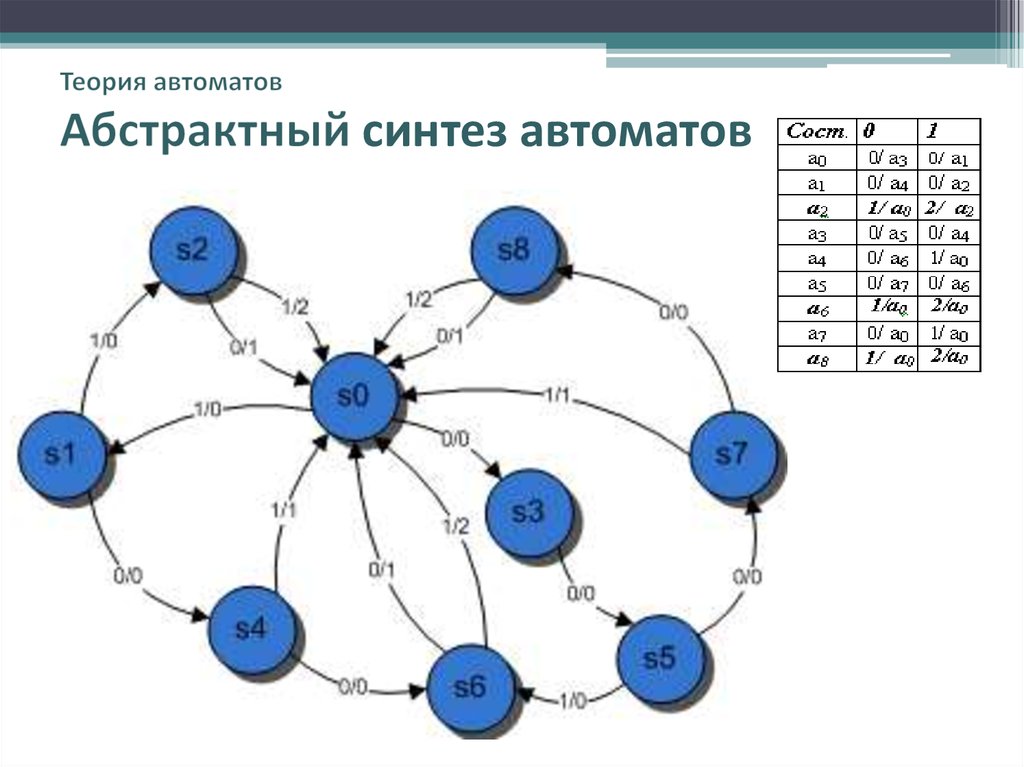
Изучите алгоритмы минимизации автоматов, чтобы лучше понять, как оптимизировать вычислительные процессы.

Математическое определение конечного автомата. Душкин объяснит


Рассмотрите примеры применения теории автоматов в реальных задачах, таких как анализ регулярных выражений и лексический анализ.

Как управлять миром, изучив всего одну простую модель!

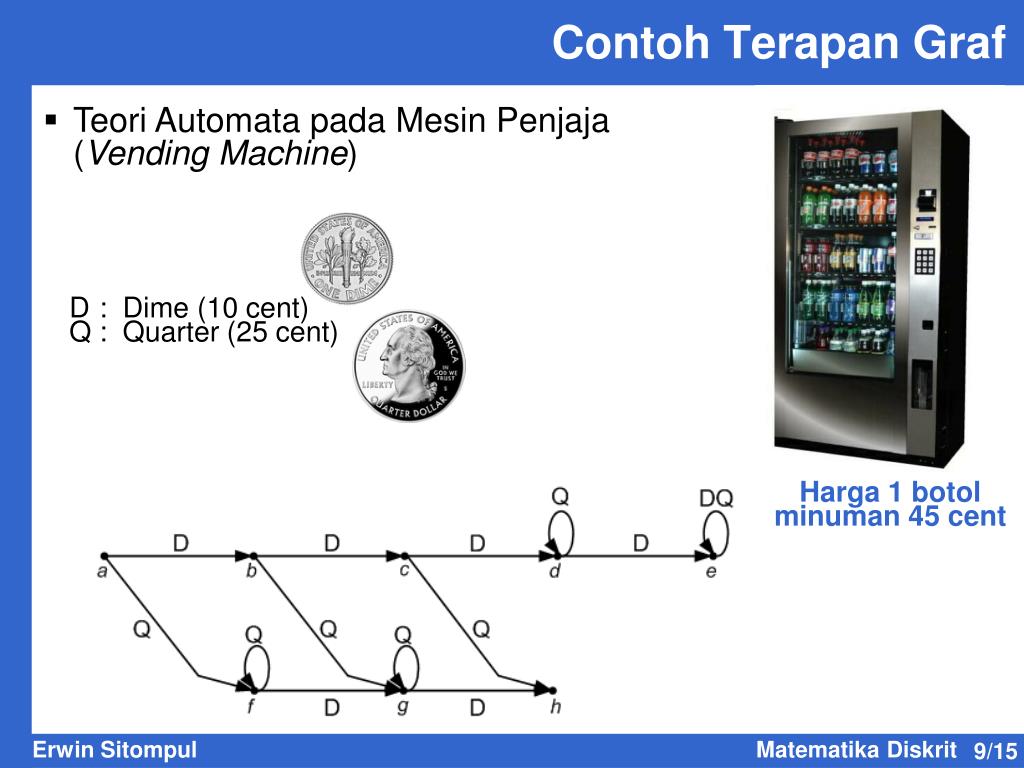
Практикуйтесь в построении автоматов для решения различных задач, чтобы закрепить теоретические знания.

Кружок - группа A - конечные автоматы, автомат КМП
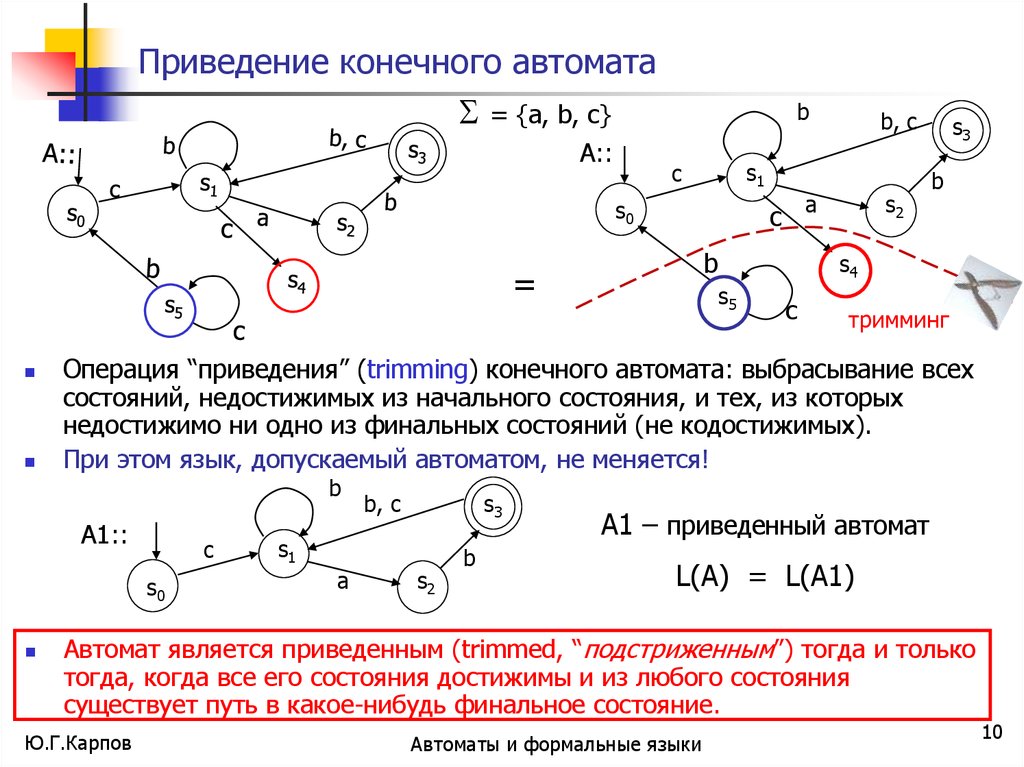
Изучите связи между теорией автоматов и другими разделами дискретной математики, такими как графы и комбинаторика.

Дискретный анализ 2. (n, r, s)-граф. Клики

Используйте интерактивные онлайн-ресурсы для визуализации работы автоматов и проверки своих решений.
Применяйте теорию автоматов для анализа и проектирования цифровых схем и систем управления.
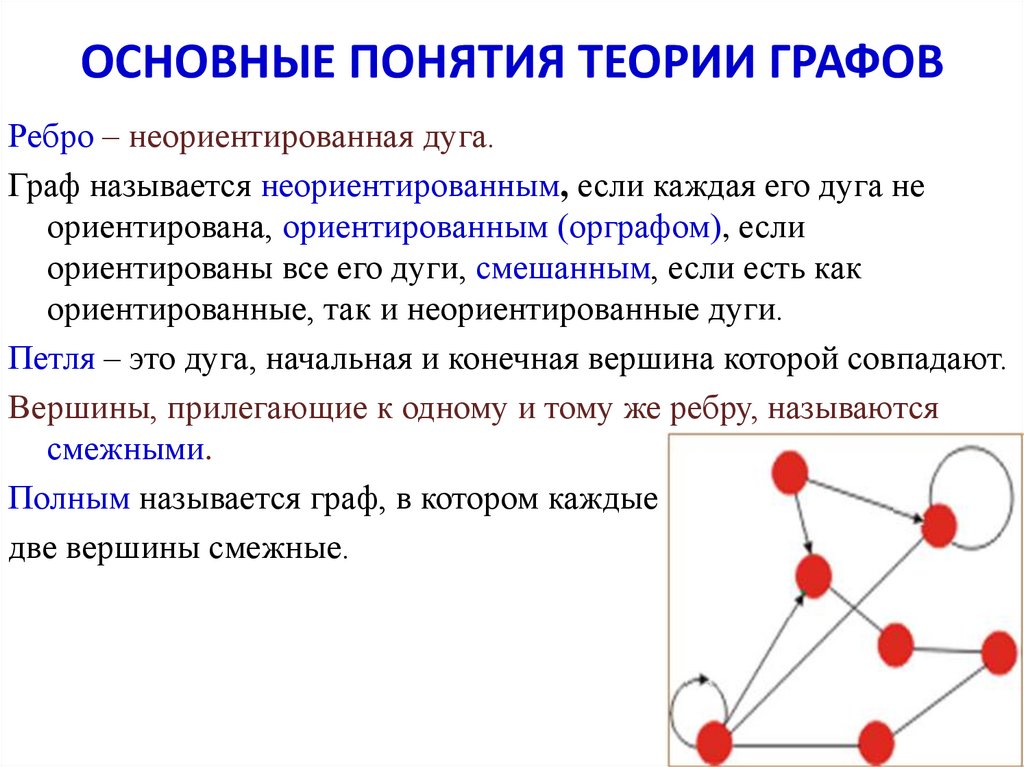
Понимание работы автоматов поможет в изучении теории языков и грамматик, что является основой для разработки компиляторов.
Рассмотрите использование автоматов в области биоинформатики для анализа последовательностей ДНК.

Изучите книги и научные статьи по теории автоматов для углубленного понимания темы и расширения кругозора.

Введение в теорию автоматов и вычислений. 1.8 пример автомата. язык автомата
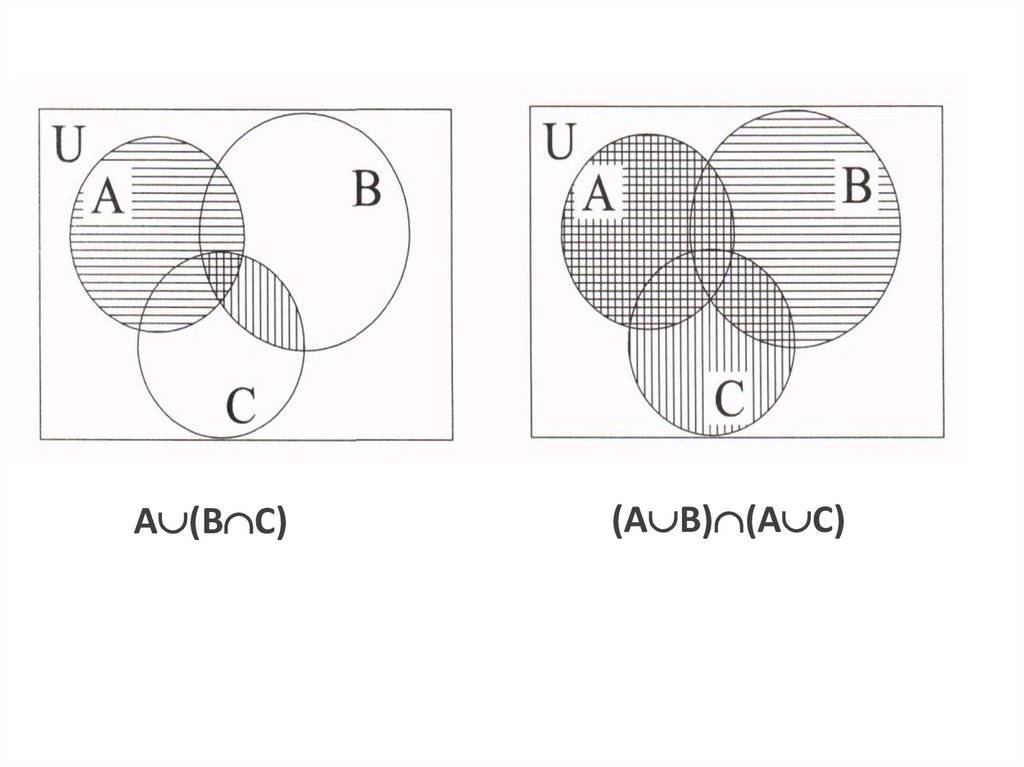
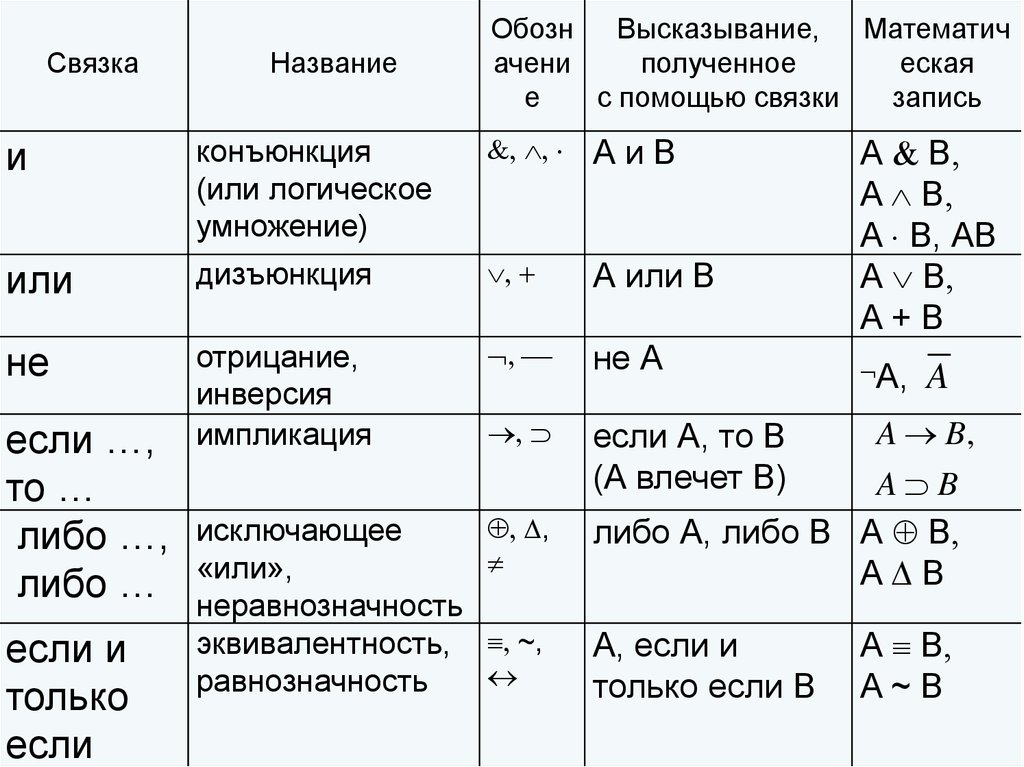

Кирилл Мокевнин, Конечные автоматы как способ значительно упростить логику и понимание кода