Всё о вписанной окружности в треугольнике: советы и факты
Вписанная окружность в треугольнике – это уникальное геометрическое явление, которое обладает множеством полезных свойств. В этой статье мы рассмотрим основные свойства, способы нахождения и практическое применение вписанной окружности.
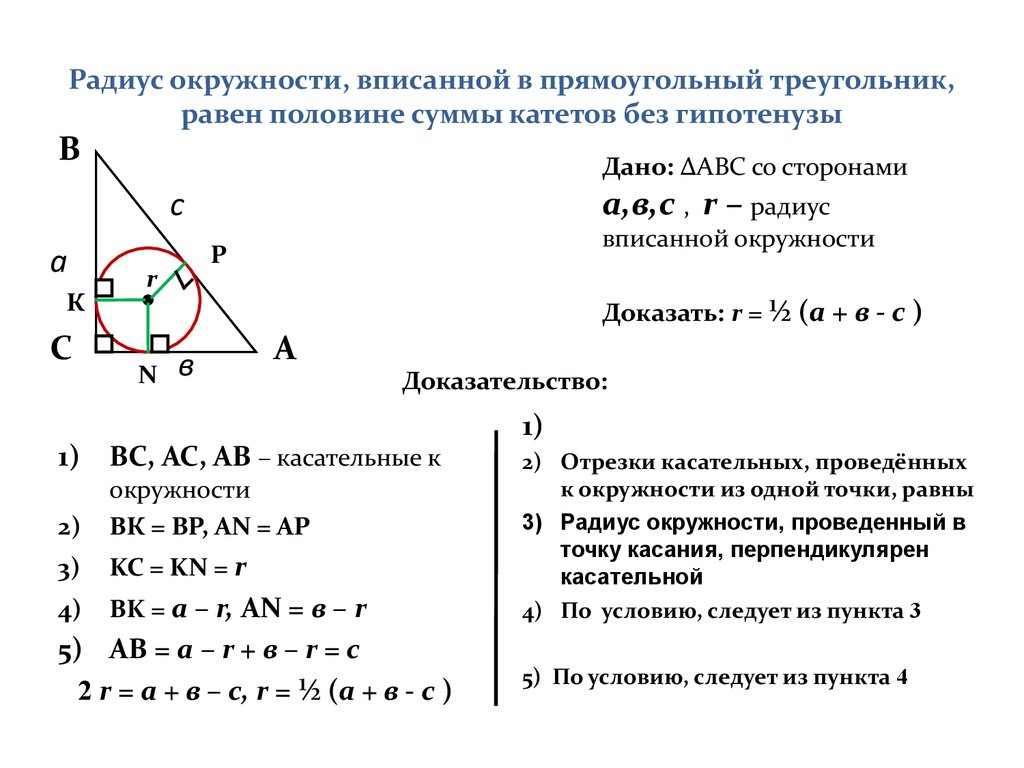
Для нахождения радиуса вписанной окружности используйте формулу: r=Apr = /frac{A}{p}r=pA, где AAA – площадь треугольника, а ppp – его полупериметр.

Вписанная и описанная окружности - Лайфхак для запоминания

Центр вписанной окружности является точкой пересечения биссектрис всех углов треугольника.

Описанная и вписанная окружности треугольника - 7 класс геометрия

Вписанная окружность касается всех сторон треугольника, поэтому она называется инцентрической.

Вписанные и описанные окружности. Вебинар - Математика

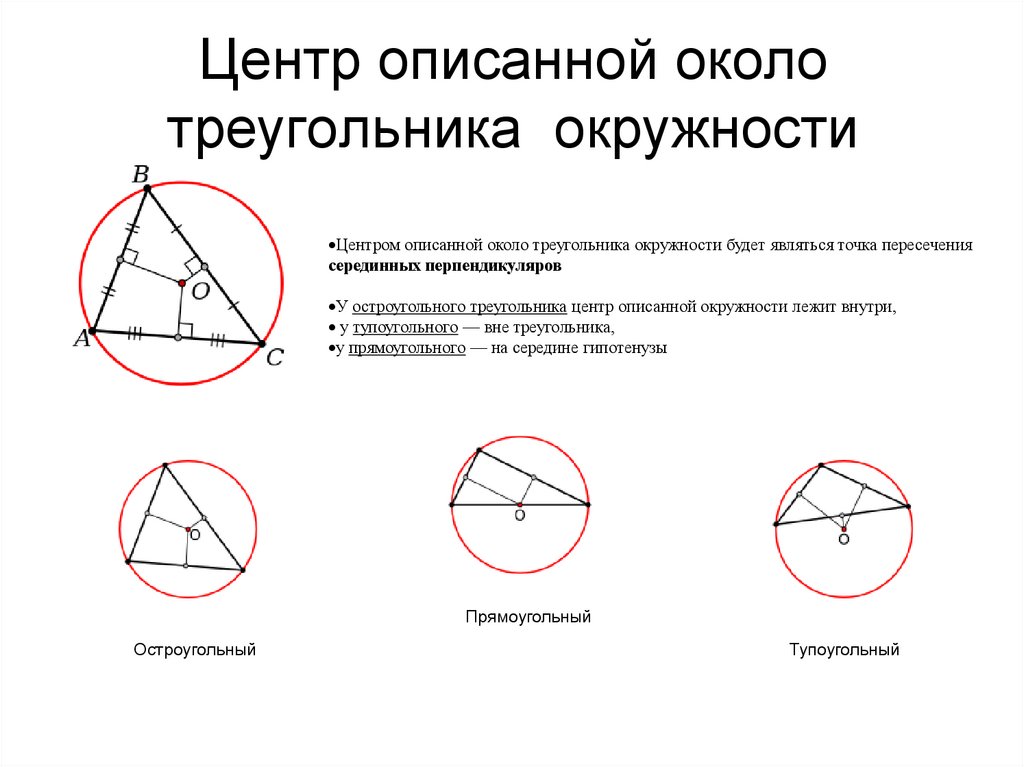
Для нахождения координат центра вписанной окружности используйте формулы: x=ax1+bx2+cx3a+b+cx = /frac{ax_1 + bx_2 + cx_3}{a + b + c}x=a+b+cax1+bx2+cx3 и y=ay1+by2+cy3a+b+cy = /frac{ay_1 + by_2 + cy_3}{a + b + c}y=a+b+cay1+by2+cy3.

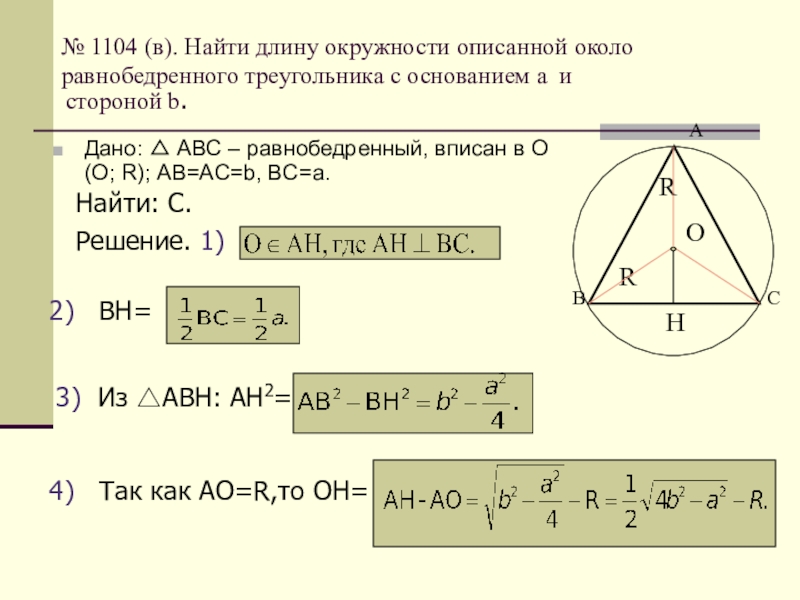
Вписанная и описанная около равнобедренного треугольника, окружность
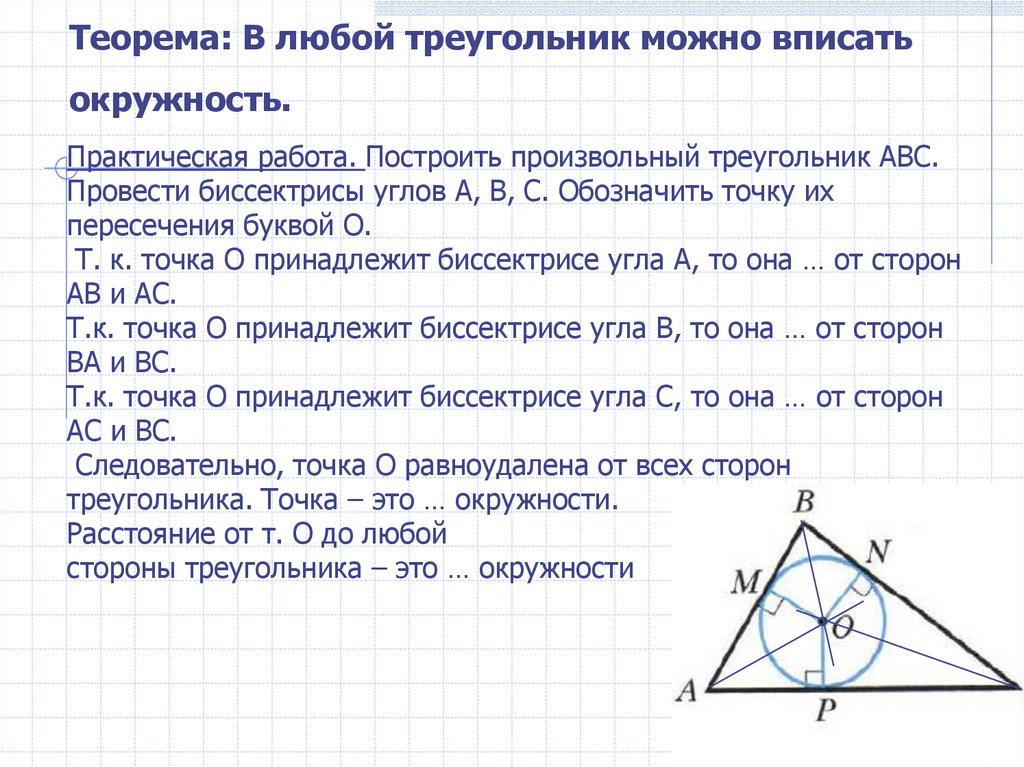
Вписанная окружность является наибольшей окружностью, которая может быть вписана в данный треугольник.

Геометрия. 7 класс. Окружности, описанная около треугольника и окружность, вписанная в треугольник
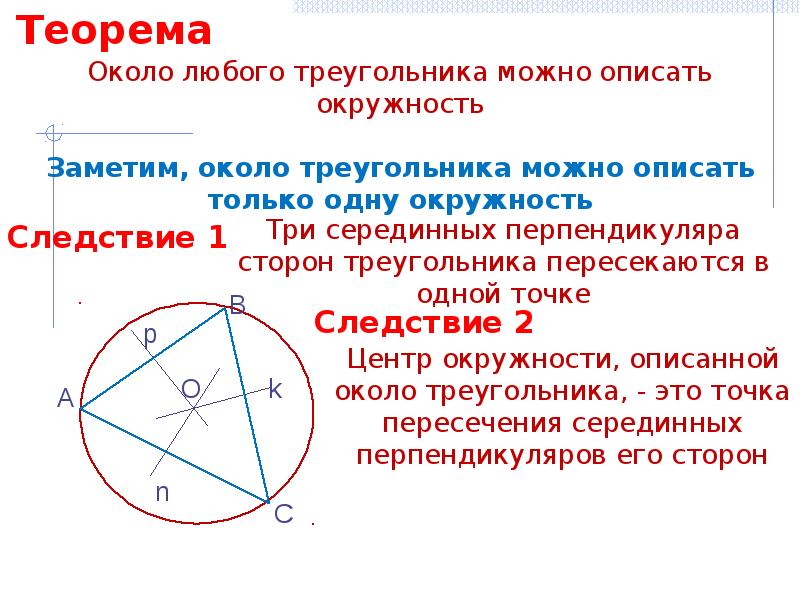

Если все стороны треугольника известны, то радиус вписанной окружности можно найти по формуле: r=(p−a)(p−b)(p−c)pr = /frac{/sqrt{(p-a)(p-b)(p-c)}}{p}r=p(p−a)(p−b)(p−c).

При конструировании треугольника и его вписанной окружности важно учитывать точность начальных данных для правильного нахождения всех элементов.
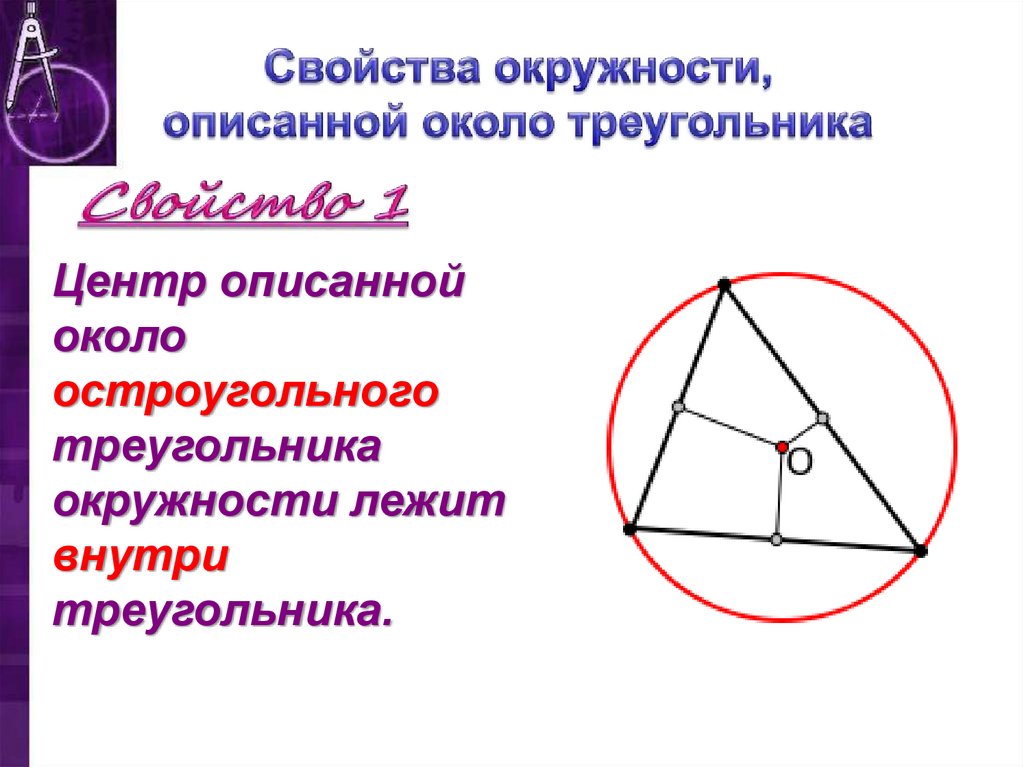
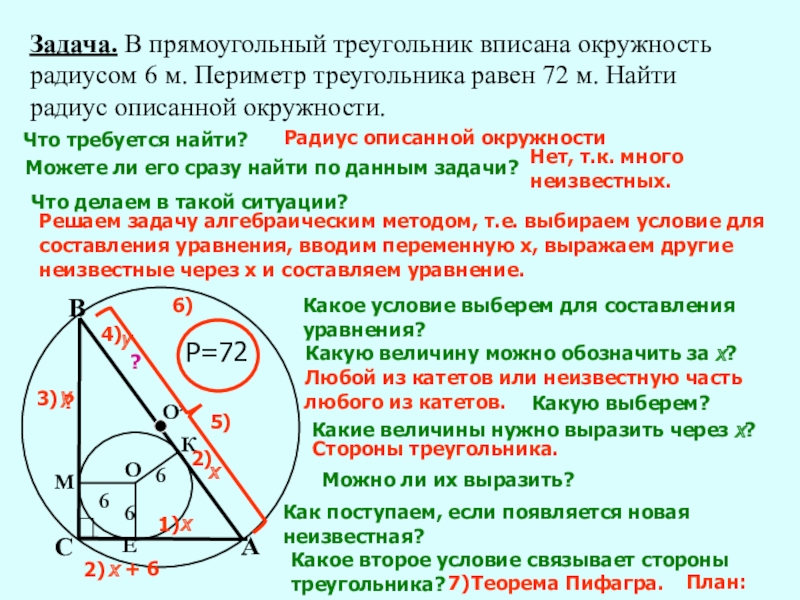
Знание свойств вписанной окружности полезно при решении задач на построение и доказательство в геометрии.

Окружность вписанная в треугольник и описанная около треугольника.
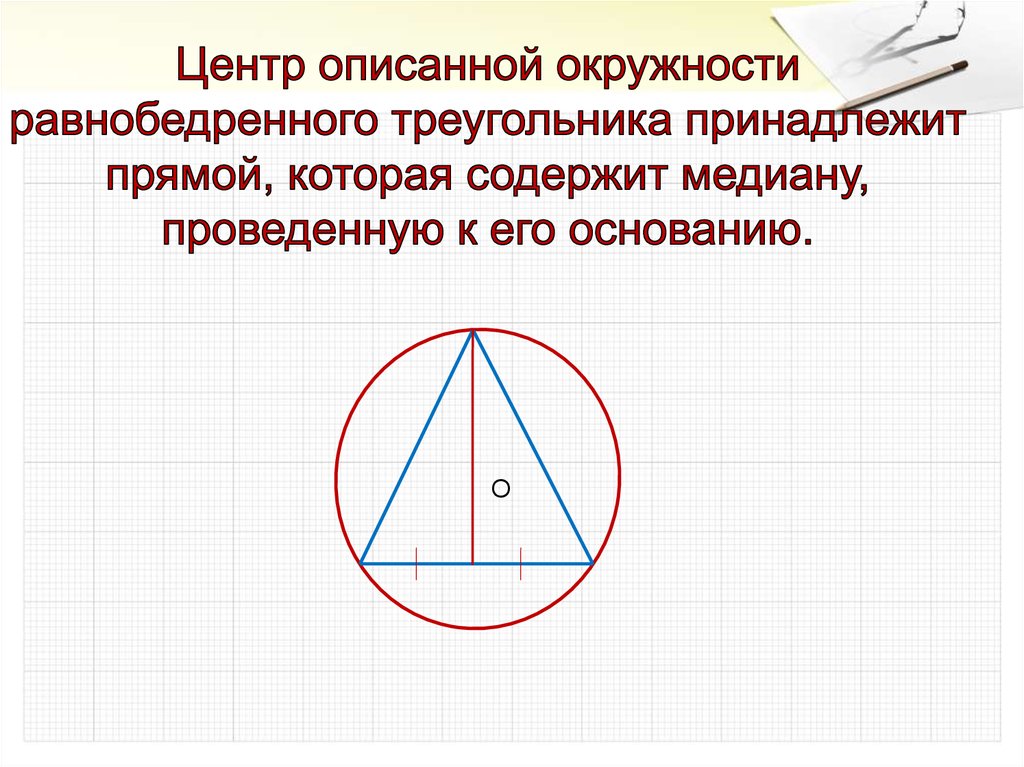
Понимание инцентрической природы окружности помогает лучше усвоить концепции треугольников и их свойств.

Окружность, вписанная в треугольник. Как найти центр и радиус. Геометрия 7-8 класс

Практическое применение знаний о вписанной окружности возможно в архитектуре и инженерных проектах.

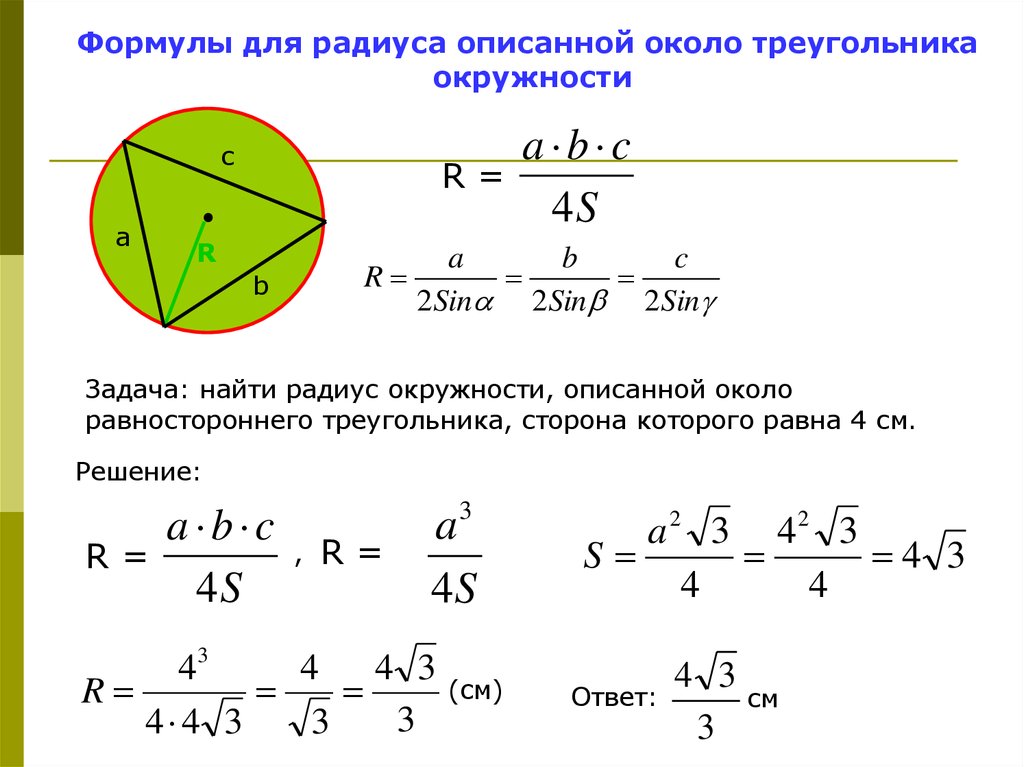
Геометрия 9 класс. Радиус описанной и вписанной окружности треугольника. Формулы радиуса.
