Как использовать ступенчатую матрицу Гаусса для решения линейных уравнений
Ступенчатая матрица Гаусса является мощным инструментом для решения систем линейных уравнений. В этой статье вы найдете полезные советы и фотографии, которые помогут вам понять и применить этот метод на практике.



Всегда начинайте с приведения матрицы к ступенчатому виду, чтобы упростить процесс решения.

Линейная алгебра, 9 урок, Метод Гаусса

Используйте элементарные преобразования строк для достижения ступенчатого вида матрицы.

Решение системы уравнений методом Гаусса
Следите за тем, чтобы главный элемент в каждой строке был ненулевым.

Линейная алгебра, Матрицы: Метод Гаусса. Высшая математика


Если в строке есть нулевые элементы, переместите их в конец строки.

Метод Гаусса. Прямой ход методом Гаусса. Обратный ход. Ступенчатая и треугольная расширенная матрица
При необходимости меняйте местами строки матрицы для упрощения процесса приведения к ступенчатому виду.

Метод Жордана-Гаусса (метод прямоугольников). Видеоурок


После приведения матрицы к ступенчатому виду приступайте к обратному ходу метода Гаусса для нахождения решений.

Метод Гаусса. Элементарные преобразования. Ранг матрицы. Ступенчатая матрица. Эквивалентная матрица
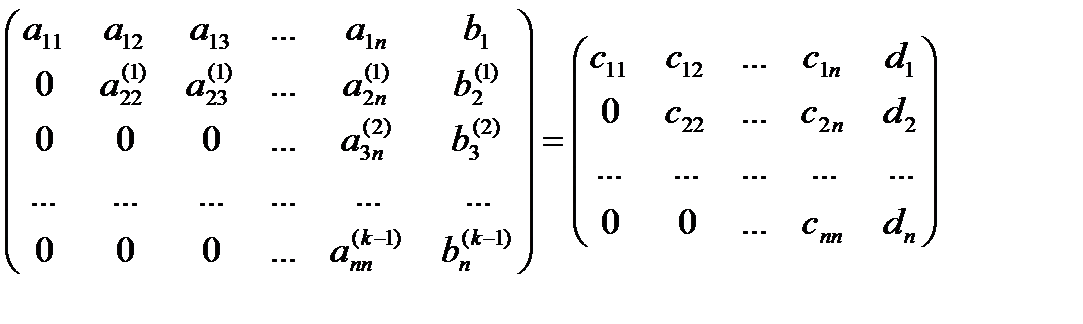
Записывайте промежуточные результаты, чтобы избежать ошибок и облегчить проверку.

Как привести матрицу к ступенчатому виду - bezbotvy
Используйте программное обеспечение или калькулятор для работы с большими матрицами.

Математика без Ху%!ни. Метод Гаусса. Совместность системы. Ранг матрицы.

Проверяйте полученные решения, подставляя их обратно в исходную систему уравнений.

Практикуйтесь на различных системах уравнений, чтобы улучшить свои навыки работы с матрицами.
