Как различать совместные и несовместные системы линейных уравнений
На этой странице вы найдете подборку фотографий и полезных советов по решению систем линейных уравнений, как совместных, так и несовместных. Эти советы помогут вам лучше понять методы и техники, используемые для решения таких систем.



Всегда проверяйте определитель матрицы системы. Если он равен нулю, система может быть несовместной или иметь бесконечное множество решений.

Совместные и несовместные системы уравнений


Для совместной системы ищите одно единственное решение, которое удовлетворяет всем уравнениям одновременно.

Общее, частное, базисное решение системы линейных уравнений Метод Гаусса

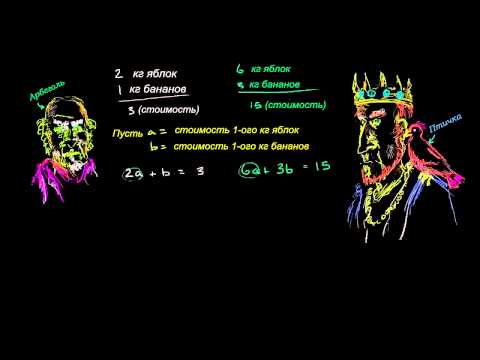
Используйте метод подстановки для упрощения системы уравнений, постепенно заменяя переменные.
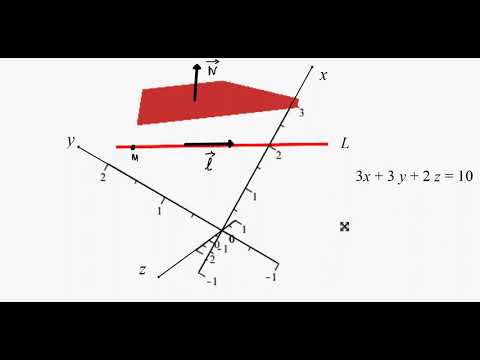
622. Несовместная система линейных алгебраических уравнений

Метод Гаусса является эффективным способом приведения системы уравнений к треугольному виду для последующего решения.

Математика без Ху%!ни. Метод Гаусса. Совместность системы. Ранг матрицы.

Если система несовместна, уравнения будут противоречивыми, например, 0 = 1.
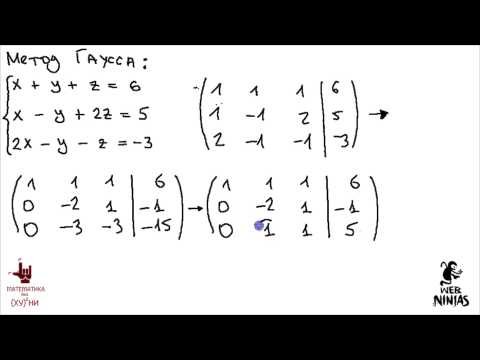
Математика без Ху%!ни. Метод Гаусса.


Метод Крамера удобен для решения систем с числом уравнений, равным числу переменных, при условии, что определитель системы не равен нулю.

Решение систем линейных уравнений методом Гаусса. Несовместные системы.

Использование матричных методов позволяет автоматизировать процесс решения системы уравнений, особенно в случае больших систем.

Исследование систем линейных уравнений на совместность

Всегда проверяйте полученные решения подставкой их обратно в исходные уравнения, чтобы убедиться в их корректности.

Графический метод решения позволяет визуально представить систему уравнений и определить количество решений.
Несовместные системы уравнений


Если система имеет бесконечное множество решений, определите общее решение через параметрическое представление.


Решение систем линейных уравнений Несовместные системы