Скалярное произведение векторов: основные формулы и полезные советы
Скалярное произведение двух векторов является важным понятием в математике и физике. Оно позволяет определить угол между векторами и вычислить различные физические величины, такие как работа или энергия. В этой статье мы рассмотрим формулы для вычисления скалярного произведения, а также дадим полезные советы для более глубокого понимания темы.


Скалярное произведение двух векторов можно вычислить как сумму произведений их соответствующих компонент: a · b = a1 * b1 + a2 * b2 + ... + an * bn.

Скалярное произведение векторов Практика


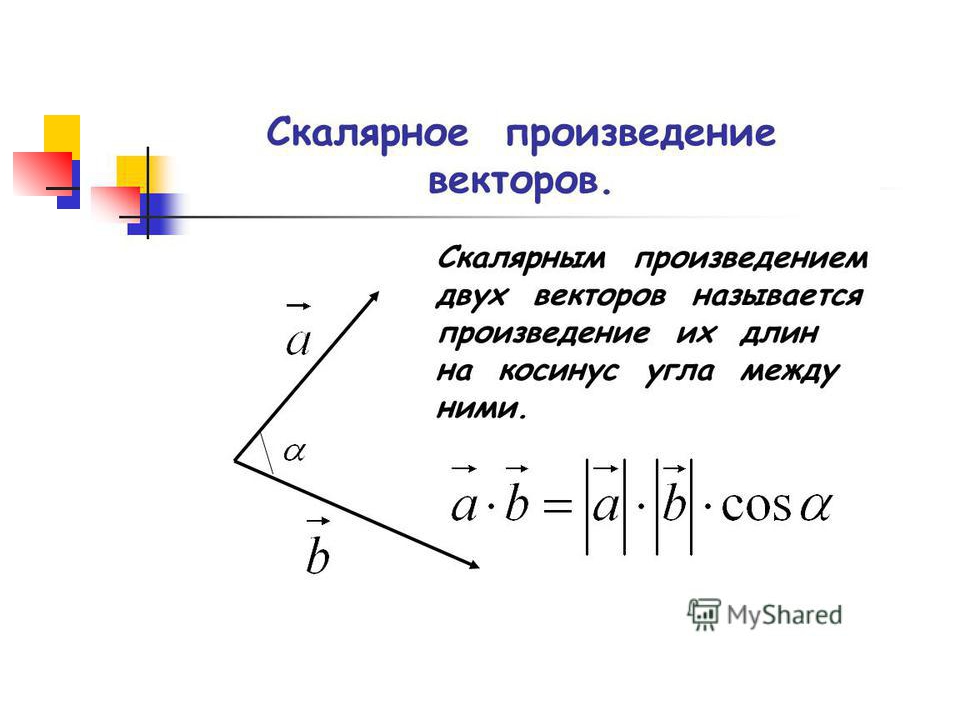
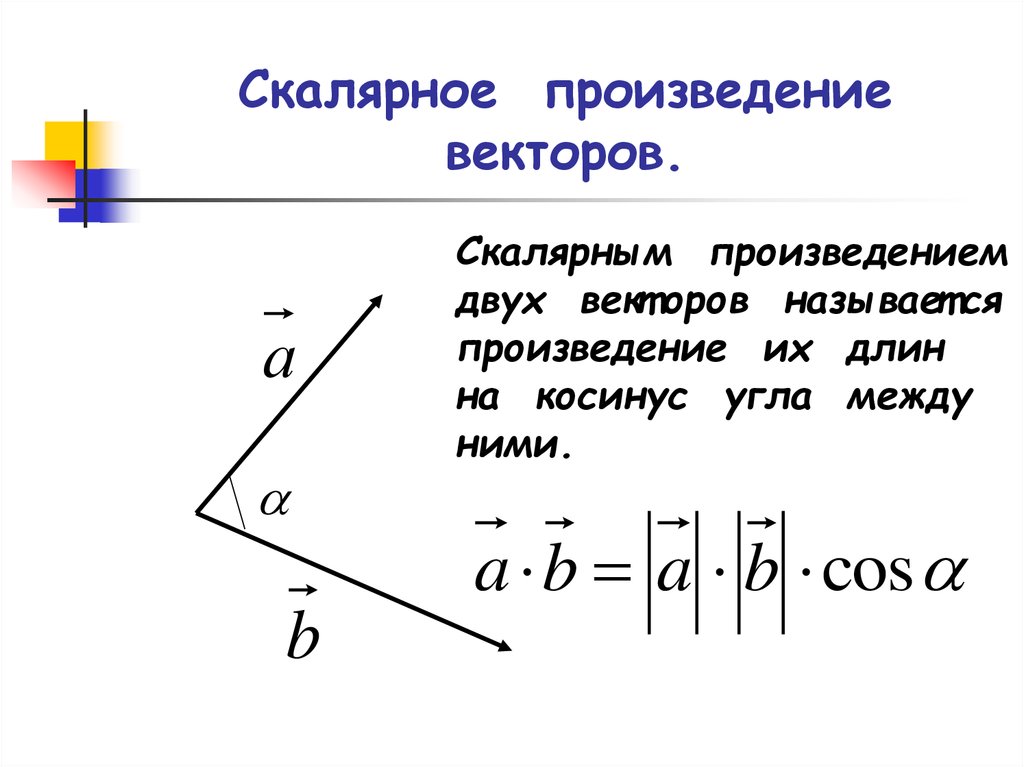
Если векторы заданы своими длинами и углом между ними, скалярное произведение можно найти по формуле: a · b = |a| * |b| * cos(θ).

A.7.2 Скалярное произведение векторов - это просто!


Используйте скалярное произведение для проверки перпендикулярности векторов: если a · b = 0, то векторы перпендикулярны.
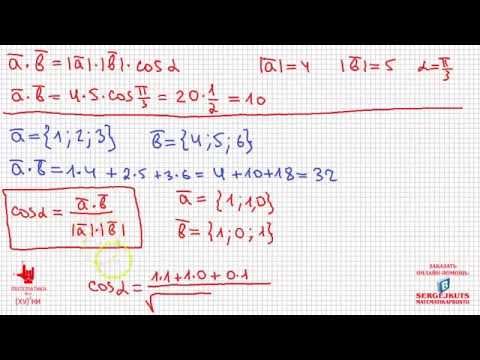
18+ Математика без Ху%!ни. Скалярное произведение векторов. Угол между векторами.

Скалярное произведение можно использовать для вычисления проекции одного вектора на другой: proj_a(b) = (a · b / |a|^2) * a.

Скалярное произведение векторов

Помните, что скалярное произведение векторов является коммутативным: a · b = b · a.

Скалярное произведение векторов.


Векторное пространство должно быть евклидовым, чтобы использовать стандартные формулы для скалярного произведения.

427
Понимание скалярного произведения важно для изучения ортогональных и ортонормированных векторов.

Используйте скалярное произведение для нахождения угла между векторами: cos(θ) = (a · b) / (|a| * |b|).

Скалярное произведение двух векторов
Если у вас есть два вектора в виде точек на плоскости, вы можете использовать скалярное произведение для нахождения их расстояния.

Скалярное произведение является основой для изучения многих других понятий в линейной алгебре, таких как собственные векторы и собственные значения.

Скалярное произведение векторов. 9 класс.