Формула скалярной разности векторов: теория и практика
Скалярная разность векторов — это важное понятие в математике и физике, которое позволяет найти величину разности между двумя векторами. В данной статье мы рассмотрим основные формулы, методы вычисления и примеры, которые помогут вам лучше понять и использовать это понятие.
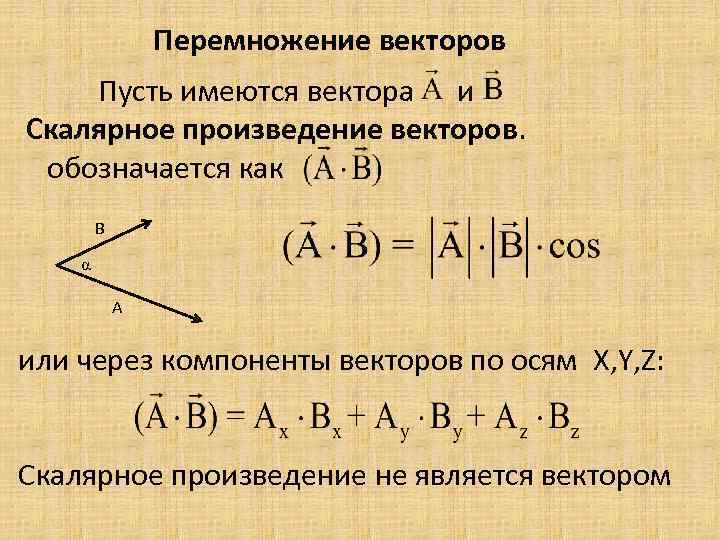
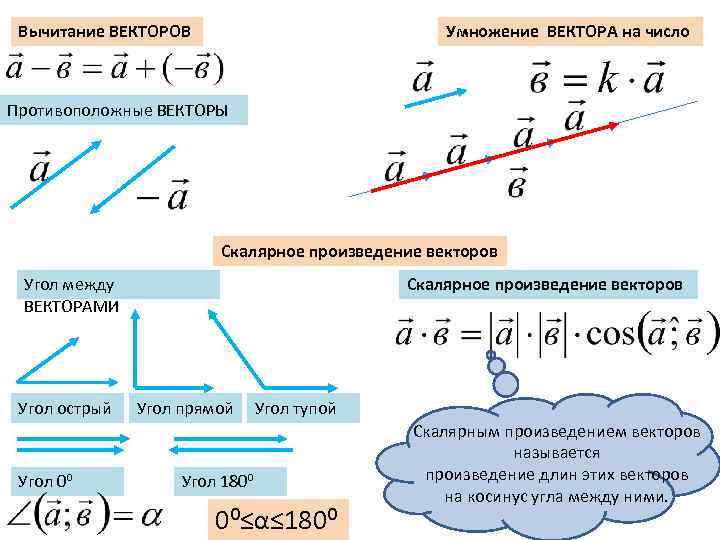
Перед началом вычислений убедитесь, что вы правильно определили направления векторов.

Зачем нужен ВЕКТОР. Объяснение смысла

Всегда проверяйте, не содержит ли ваше вычисление ошибок в знаках или знаках векторов.

Вектор. Сумма разность векторов. Скалярное произведение векторов. Координаты векторов.
Используйте диаграммы и чертежи для наглядного понимания направления и величины векторов.

РАЗНОСТЬ ВЕКТОРОВ геометрия 9 Атанасян
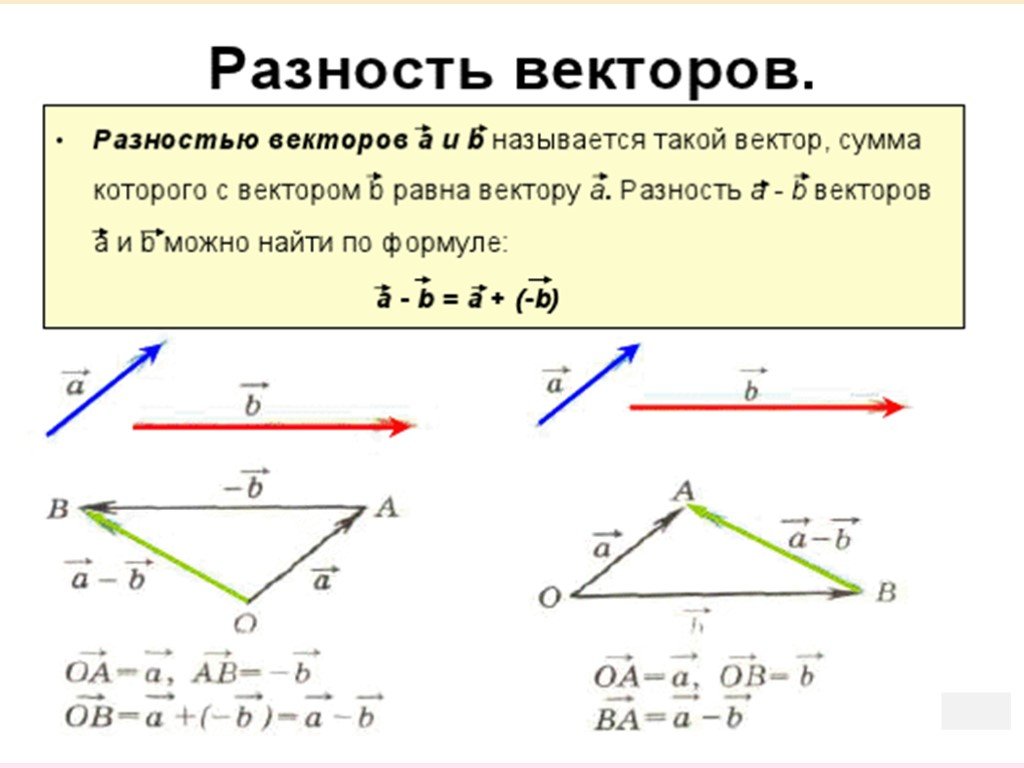
При работе с векторами полезно использовать программное обеспечение или калькуляторы для упрощения вычислений.

Скалярное произведение векторов.
Практикуйтесь на простых примерах, чтобы закрепить понимание скалярной разности векторов.

Вектор. Сложение и вычитание. 9 класс - Математика
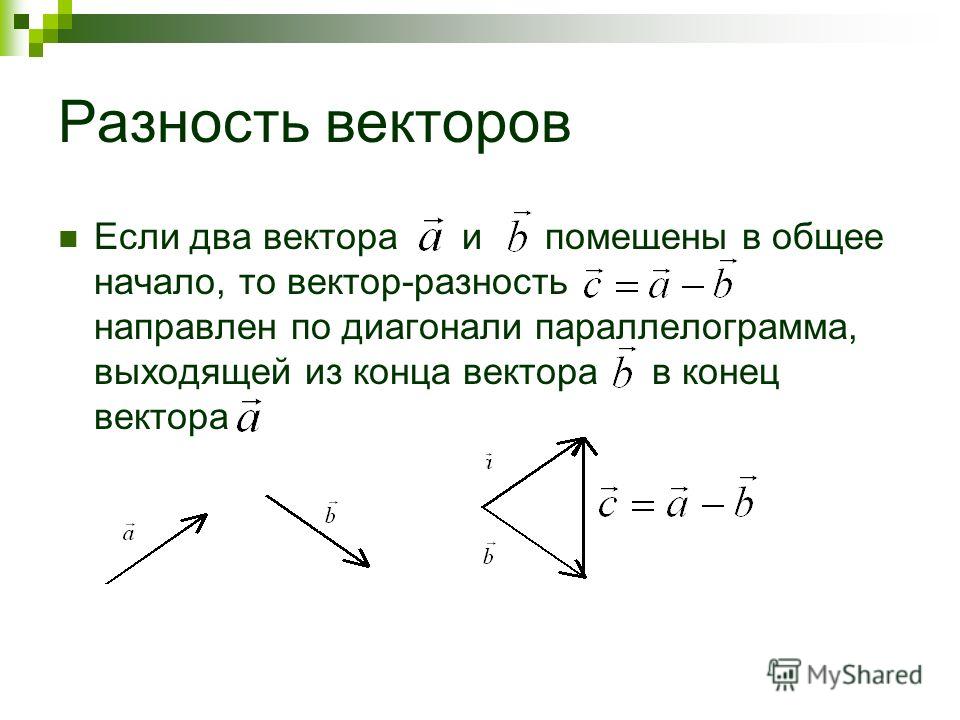
Помните, что скалярная разность может быть как положительной, так и отрицательной в зависимости от направления векторов.
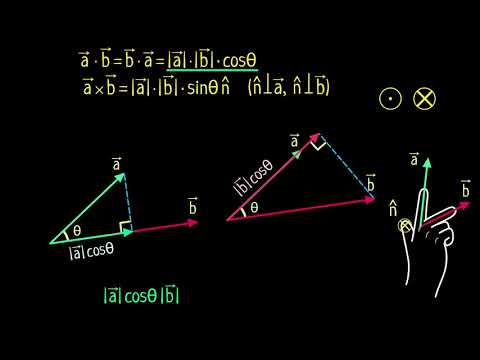
Сравнение скалярного и векторного произведений векторов (видео 16) - Магнетизм - Физика

Изучите основные свойства векторов, такие как коллинеарность и ортогональность, для лучшего понимания их взаимодействия.

ПРОСТОЙ СПОСОБ, как запомнить Векторы за 10 минут! (вы будете в шоке)
Используйте цветовую кодировку при визуализации векторов для лучшего восприятия информации.

Применяйте формулы и методы на практике, чтобы развивать навыки и уверенность в вычислениях.


Не забывайте, что теоретические знания должны подкрепляться практическими задачами и реальными примерами.


Векторы и действия над ними, проекция вектора на координатные оси. 9 класс.