Изучение равнобедренного треугольника MNO и его особенностей
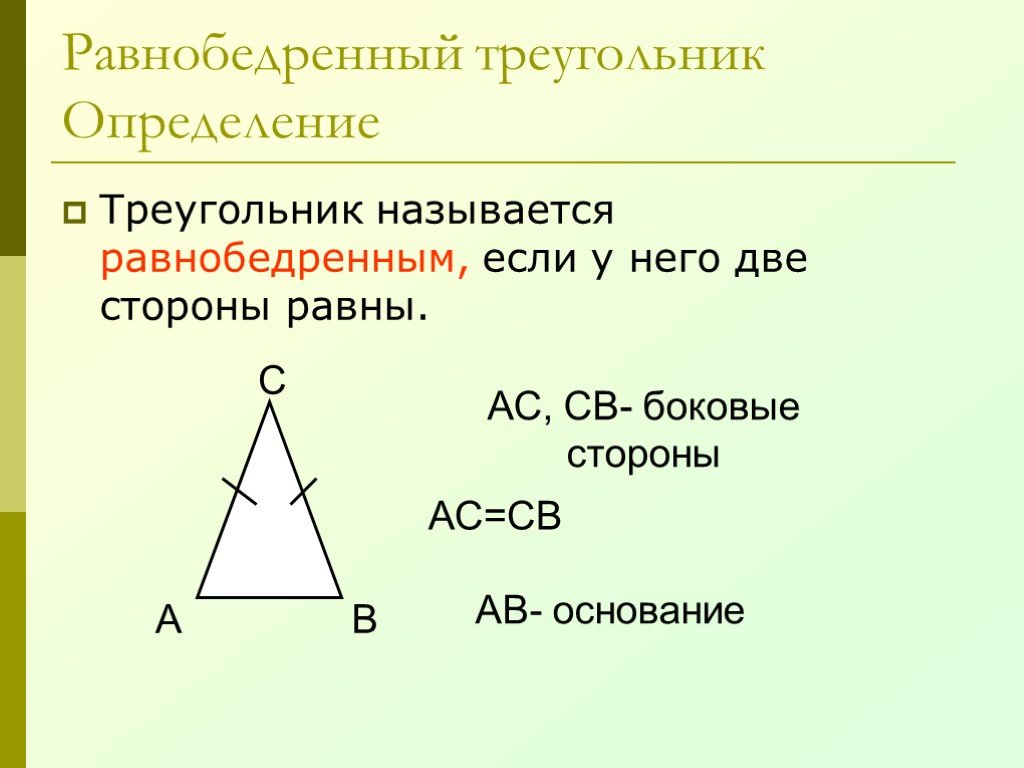
Равнобедренный треугольник MNO с основанием представляет собой уникальную фигуру, в которой две стороны равны, а третья сторона является основанием. Эта геометрическая фигура имеет ряд интересных свойств и применения в математике и инженерии.
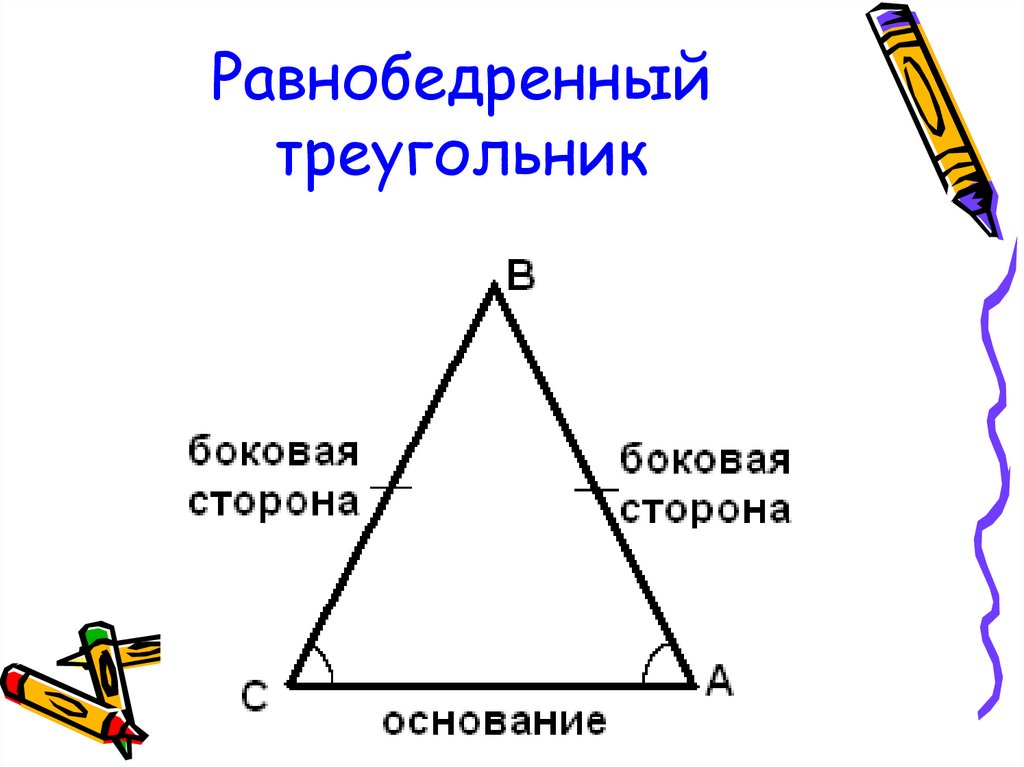

Для начала работы над задачей с равнобедренным треугольником, убедитесь, что вы правильно определили основание и равные стороны.

Равнобедренный треугольник. 7 класс.
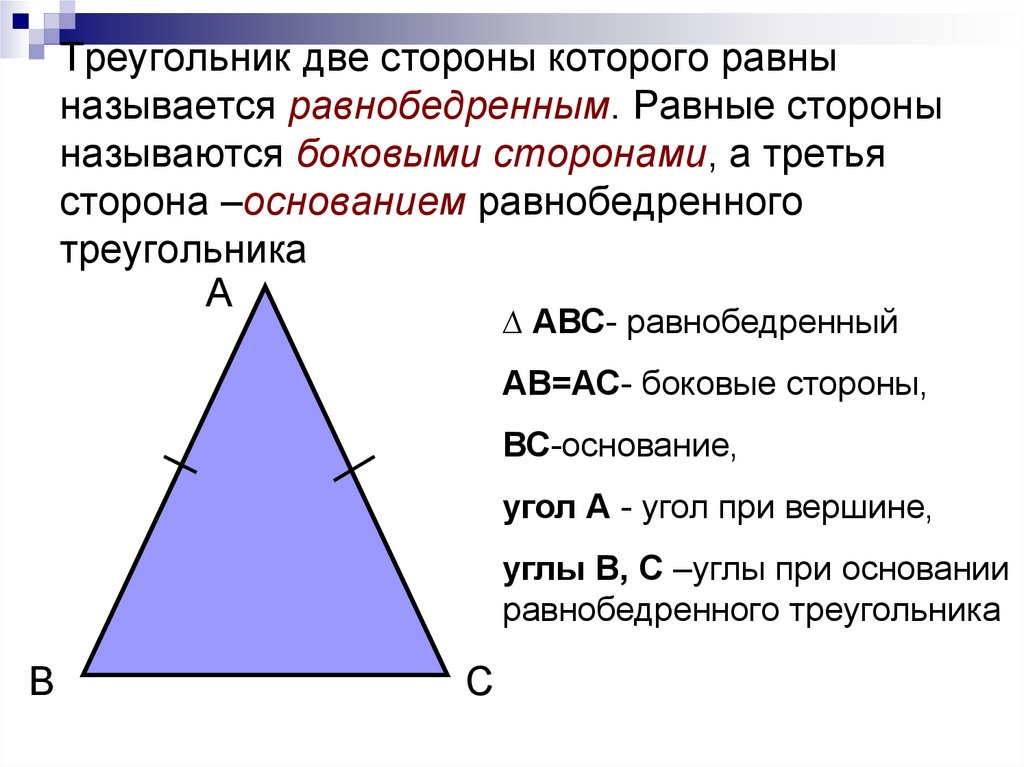
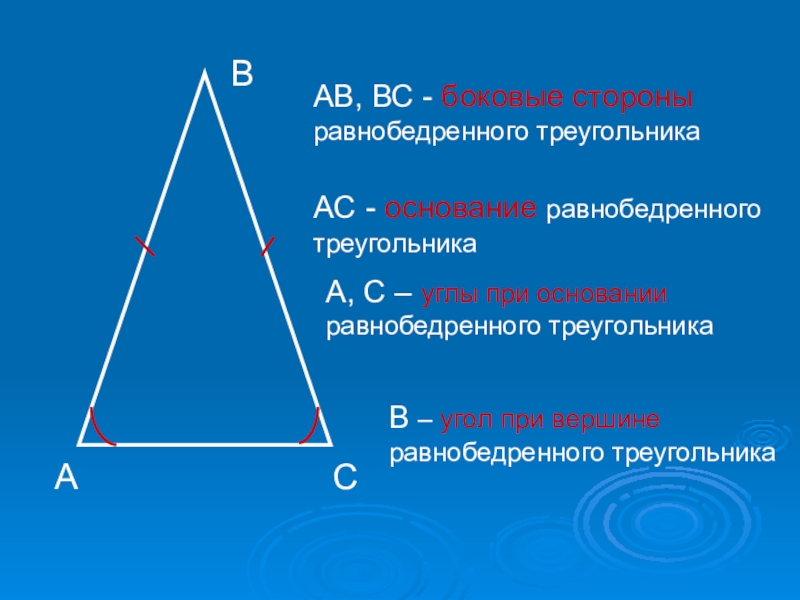
Используйте теорему Пифагора для нахождения неизвестных сторон в равнобедренном треугольнике.

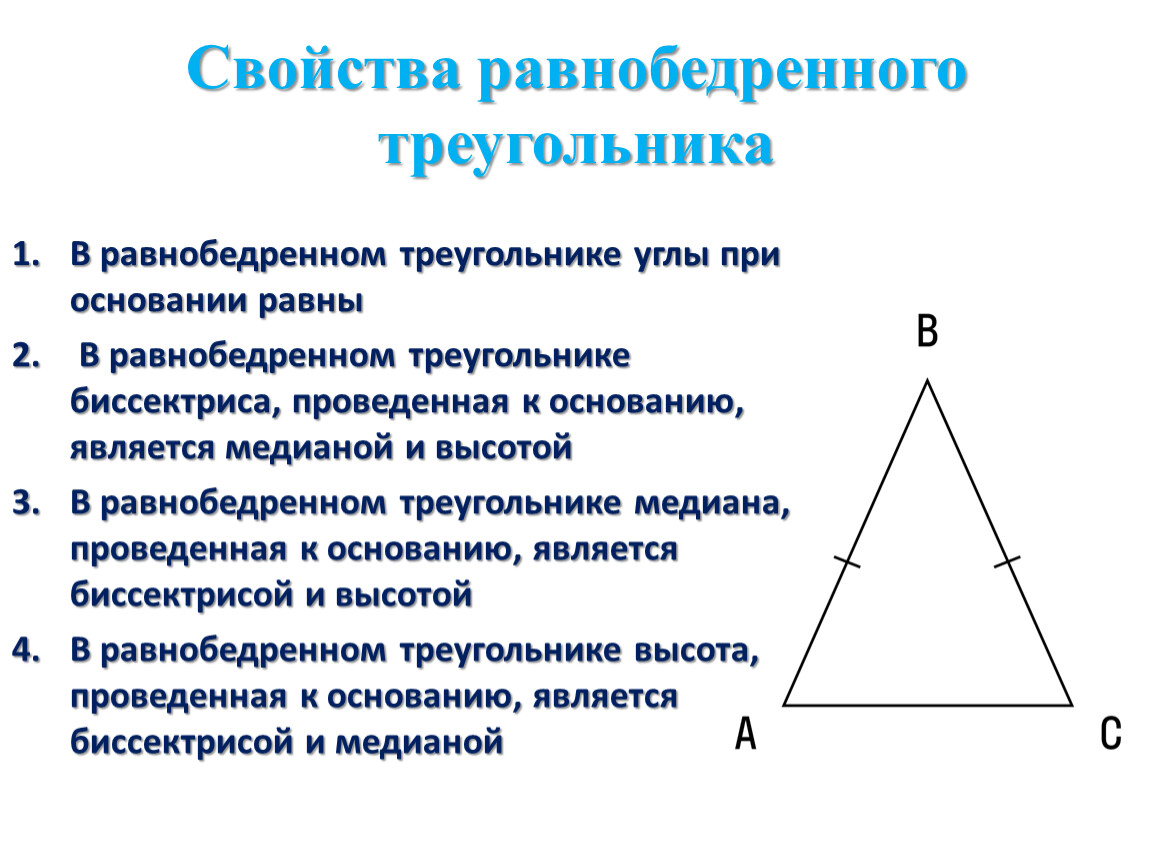
7 класс, 18 урок, Свойства равнобедренного треугольника
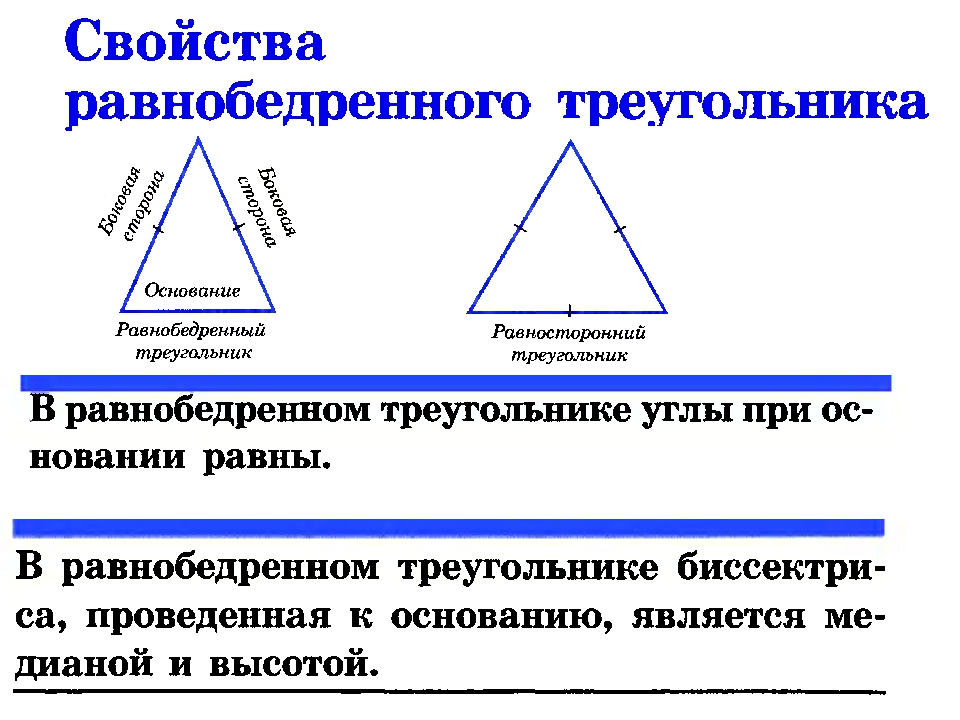

При решении задач с равнобедренным треугольником важно помнить, что углы при основании равны.

№ 308 - Геометрия 7-9 класс Атанасян

В геометрических построениях часто используется медиана, проведенная к основанию равнобедренного треугольника, которая также является его высотой.

Задача 6 №27923 ЕГЭ по математике. Урок 140

При вычислении площади равнобедренного треугольника используйте формулу 1/2 * основание * высота.

№689. В равнобедренном треугольнике основание равно 10 см, а боковая сторона равна 13 см


Обратите внимание на симметрию равнобедренного треугольника, которая может упростить решение задач.

Используйте свойства равнобедренного треугольника для доказательства теорем и решения геометрических задач.
Проверяйте правильность своих расчетов, особенно при работе с углами и длинами сторон.

Сложная задача от Атанасяна
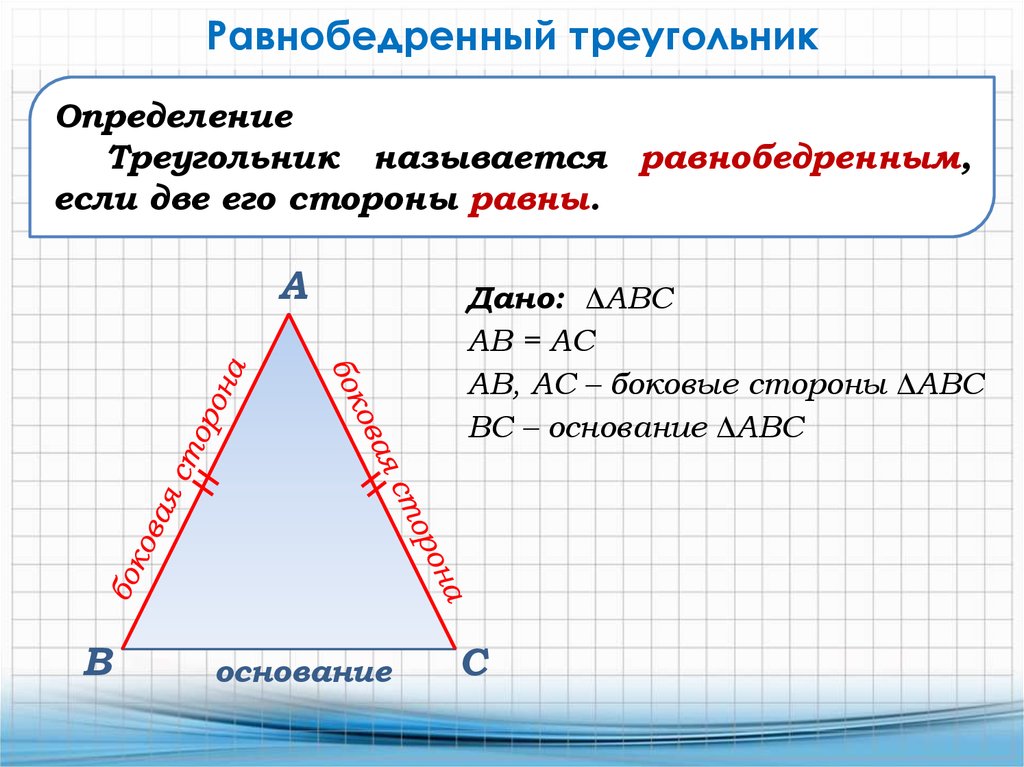
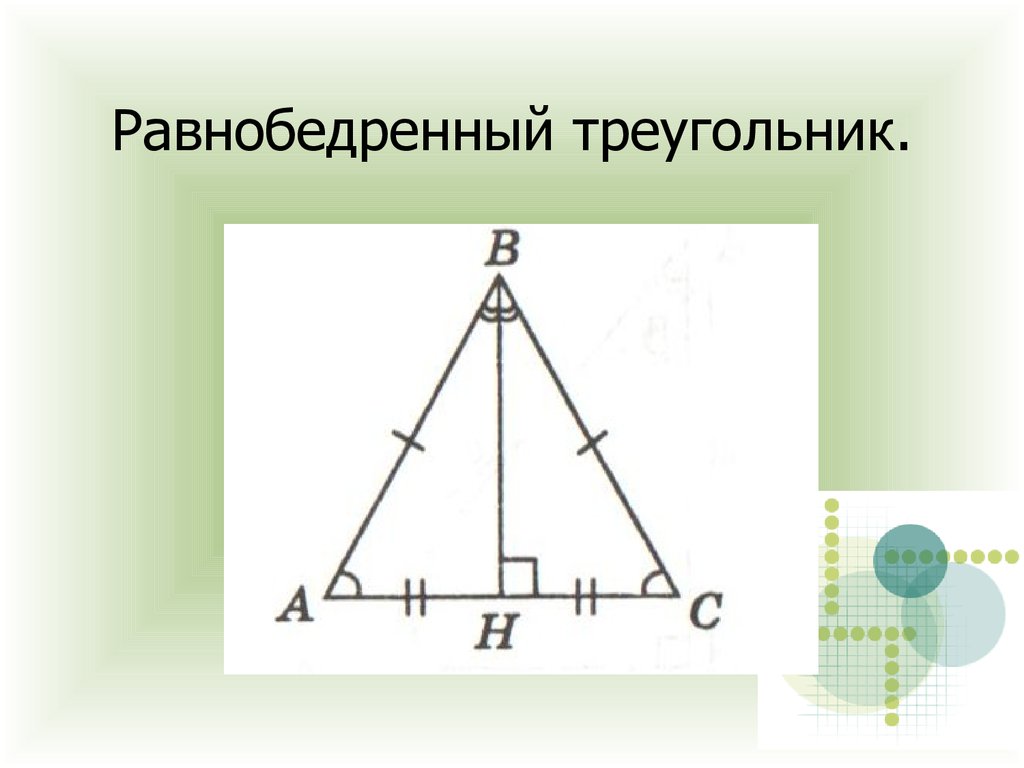
Практикуйтесь в построении равнобедренных треугольников с использованием циркуля и линейки для лучшего понимания их свойств.
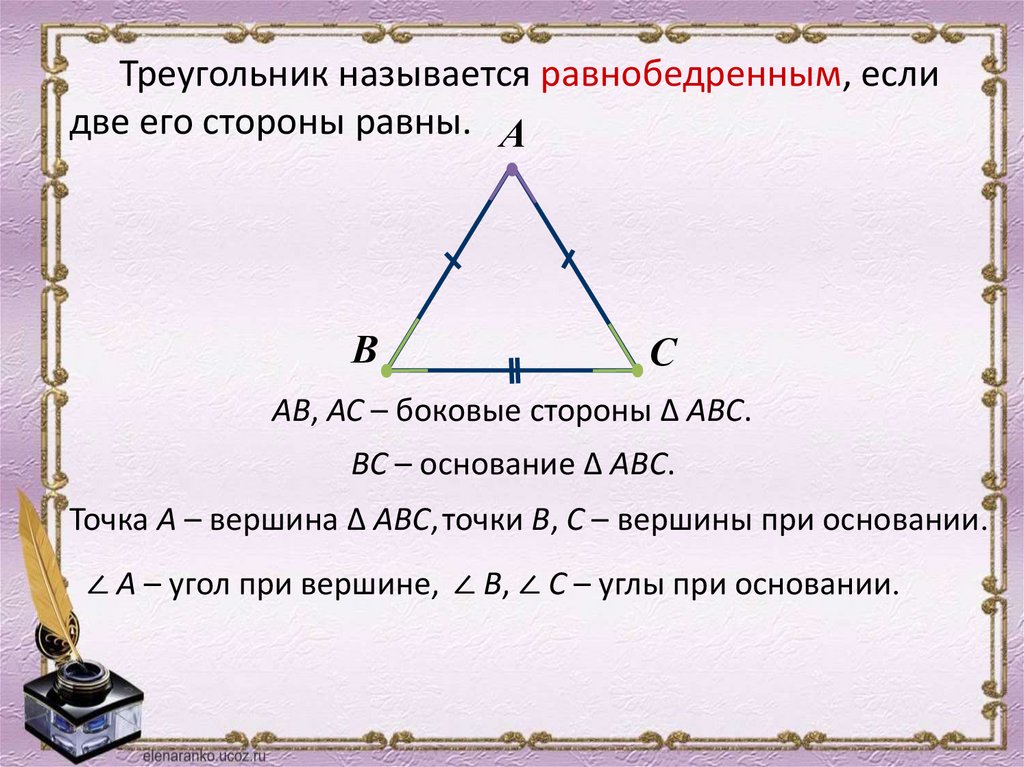
Изучайте примеры реальных приложений равнобедренных треугольников в архитектуре и инженерии для расширения своего понимания этой геометрической фигуры.
