Формула площади треугольника через синус и стороны
На этой странице вы найдете подробное описание метода вычисления площади треугольника с использованием синуса угла и двух сторон. Этот метод является полезным инструментом в геометрии и тригонометрии, позволяя быстро и точно находить площадь.
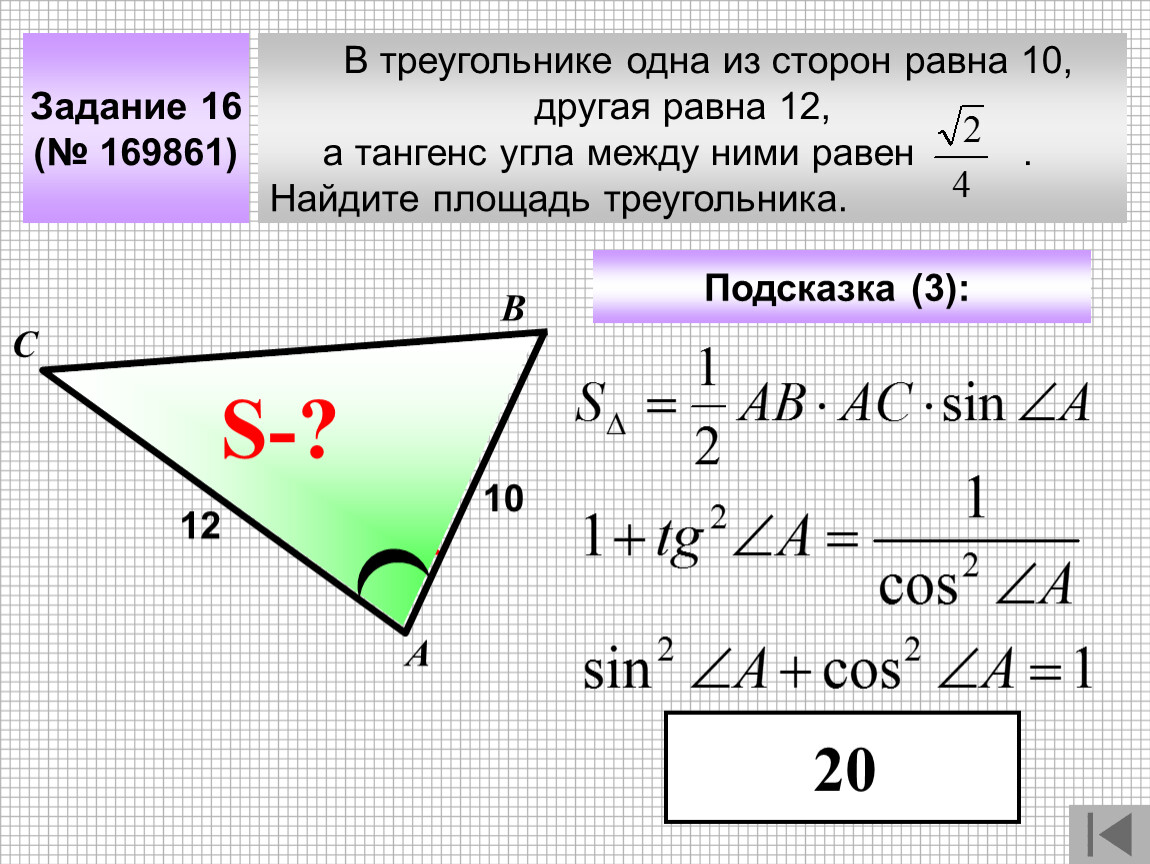
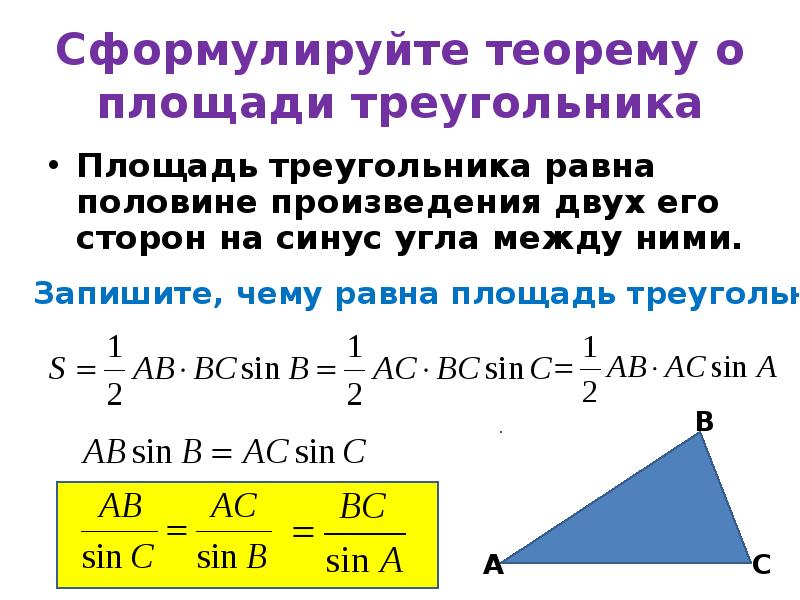

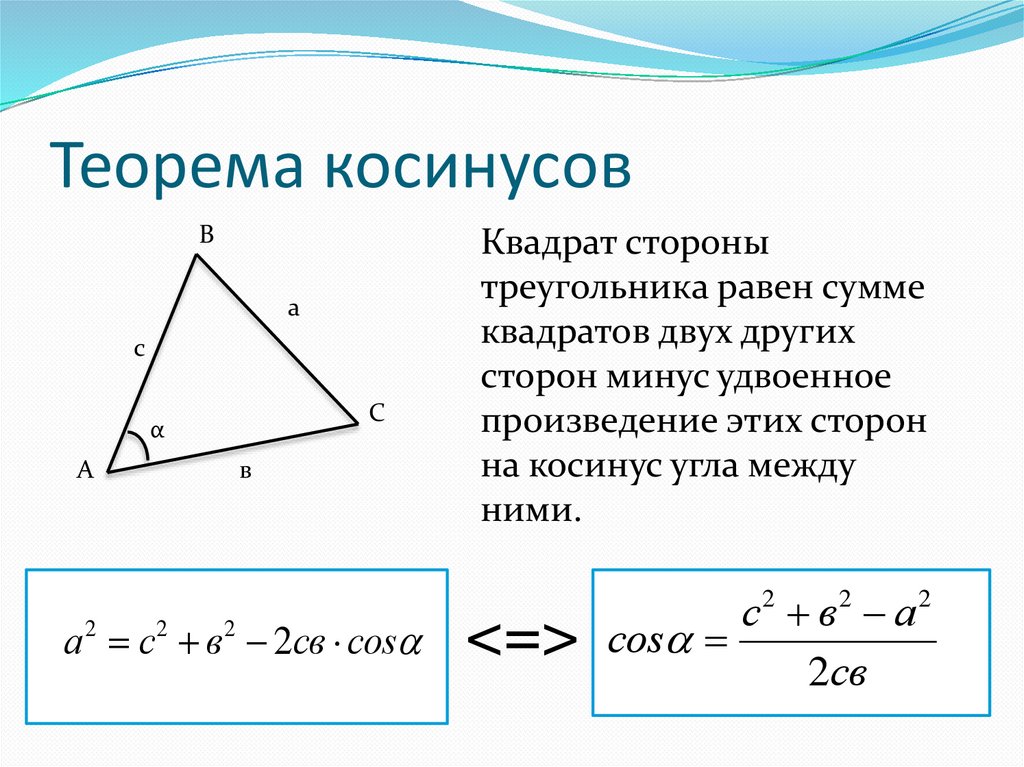
Для вычисления площади треугольника используйте формулу: S=12absin(C)S = /frac{1}{2} a b /sin(C)S=21absin(C), где aaa и bbb — стороны, а CCC — угол между ними.

Геометрия 9 класс : Теорема о площади треугольника

Убедитесь, что угол CCC измерен в радианах, если используете калькулятор, иначе результат может быть некорректным.

Найдите площадь треугольника на рисунке ★ Два способа решения
Проверяйте правильность введенных данных, особенно если стороны треугольника и угол заданы в разных единицах измерения.

✓ Новая формула площади треугольника - Ботай со мной #108 - Борис Трушин

Для точных вычислений используйте калькулятор с возможностью ввода тригонометрических функций или специализированное программное обеспечение.

Площадь треугольника и синус угла
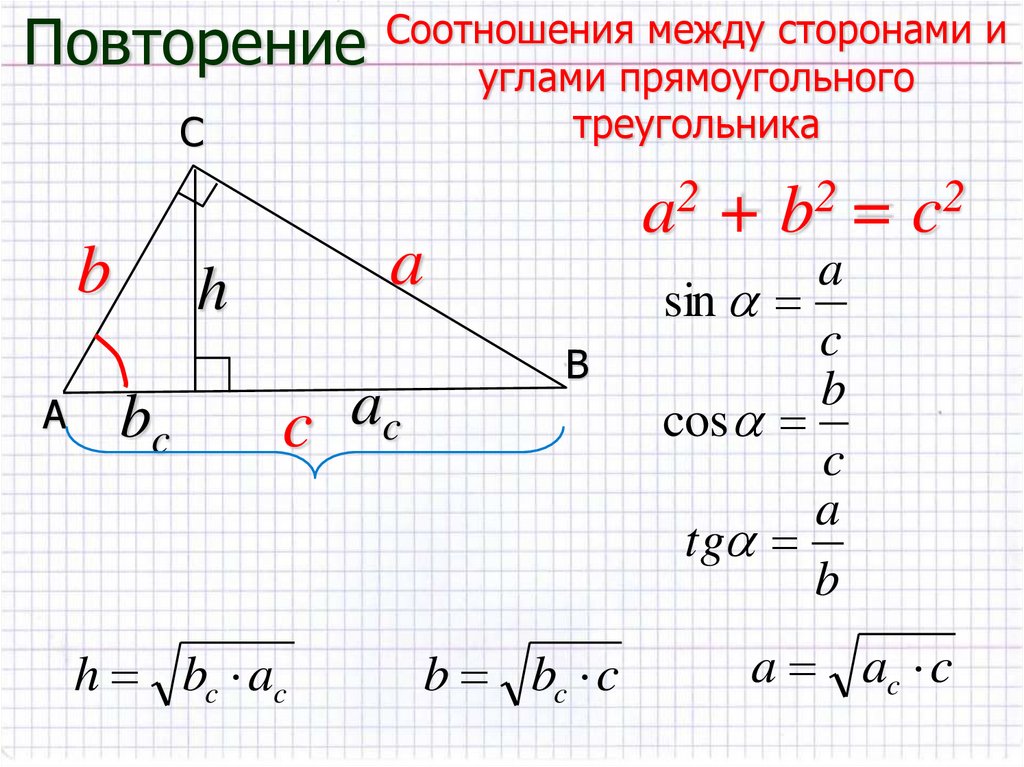
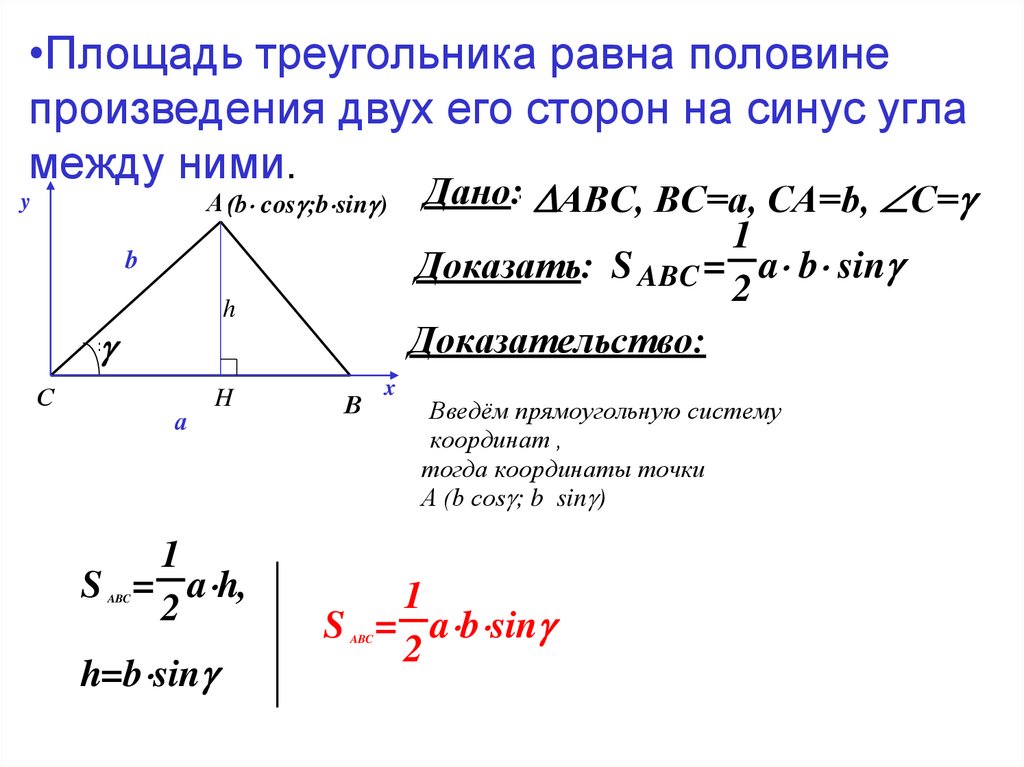
Помните, что синус угла достигает максимального значения при угле 90°, что дает наибольшую площадь треугольника.

Синус, косинус и тангенс Решение задач по геометрии
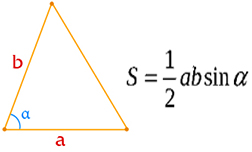
Если угол между сторонами неизвестен, вы можете использовать теорему косинусов для его нахождения.
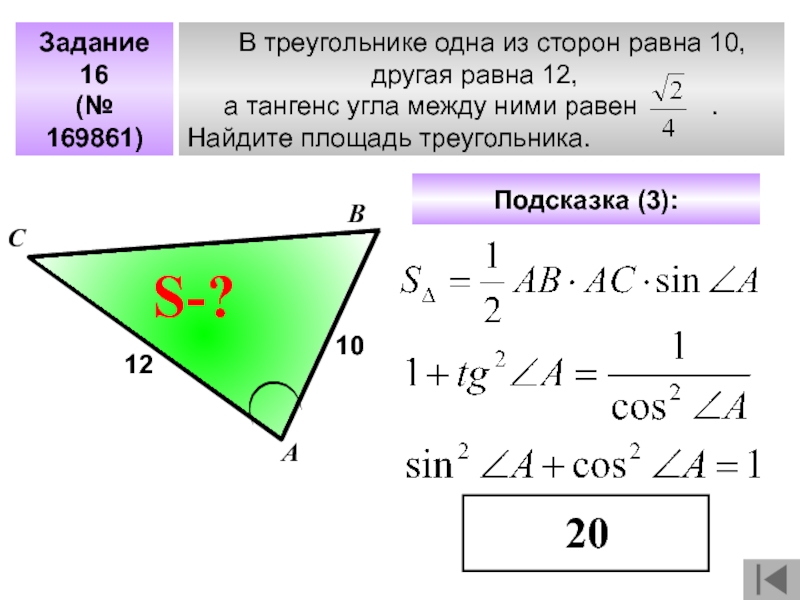
Знание этой формулы полезно при решении задач на экзаменах и в повседневной практике.
Используйте графические инструменты, такие как геометрические программы, для наглядного представления треугольников и проверки расчетов.

Банк ОГЭ/Геометрия 10 стр, №6 - Площадь треугольника по двум сторонам и углу между ними


Не забывайте о возможности ошибок округления, особенно при работе с большими числами или малыми углами.
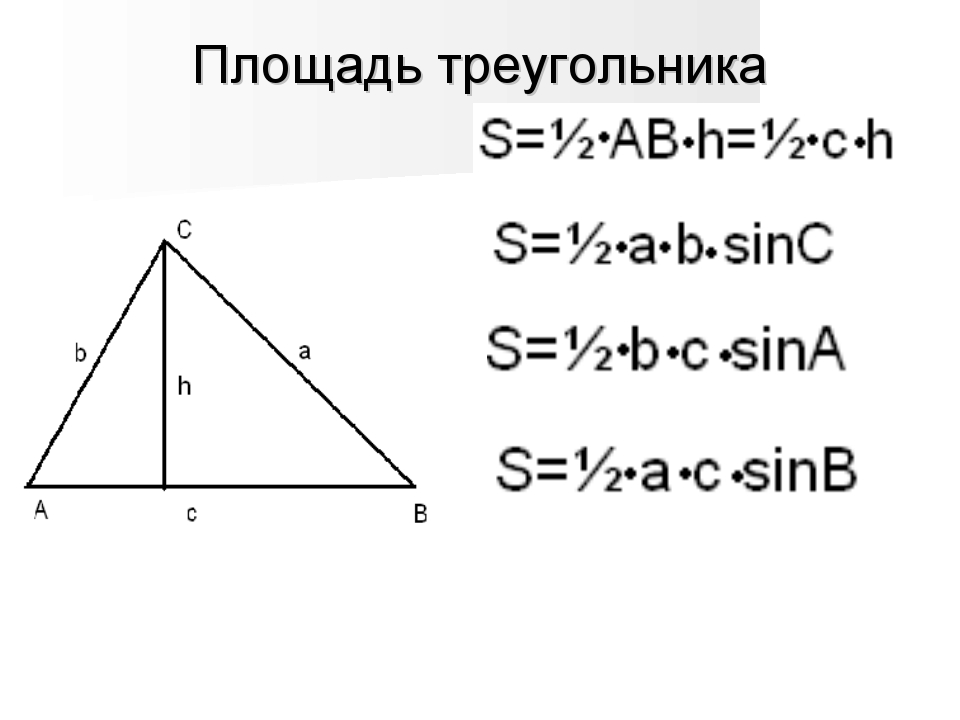
Практикуйтесь в решении различных задач с использованием этой формулы, чтобы лучше понять ее применение и свойства.

Теорема синусов с доказательством