Как найти площадь тела вращения с помощью интегралов
Площадь поверхности тела вращения через интеграл — важная тема в математике, которая помогает понять, как вычислять площадь сложных фигур. В этой статье мы рассмотрим основные методы и приведем полезные советы для решения подобных задач.



Начните с простых примеров для понимания базовых принципов.
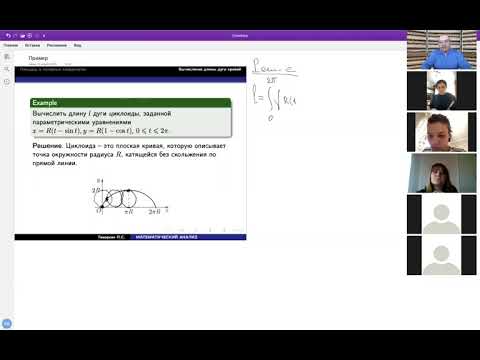
Вычисление длины дуги кривой в параметрических и полярных координатах. Вычисление объема тела.
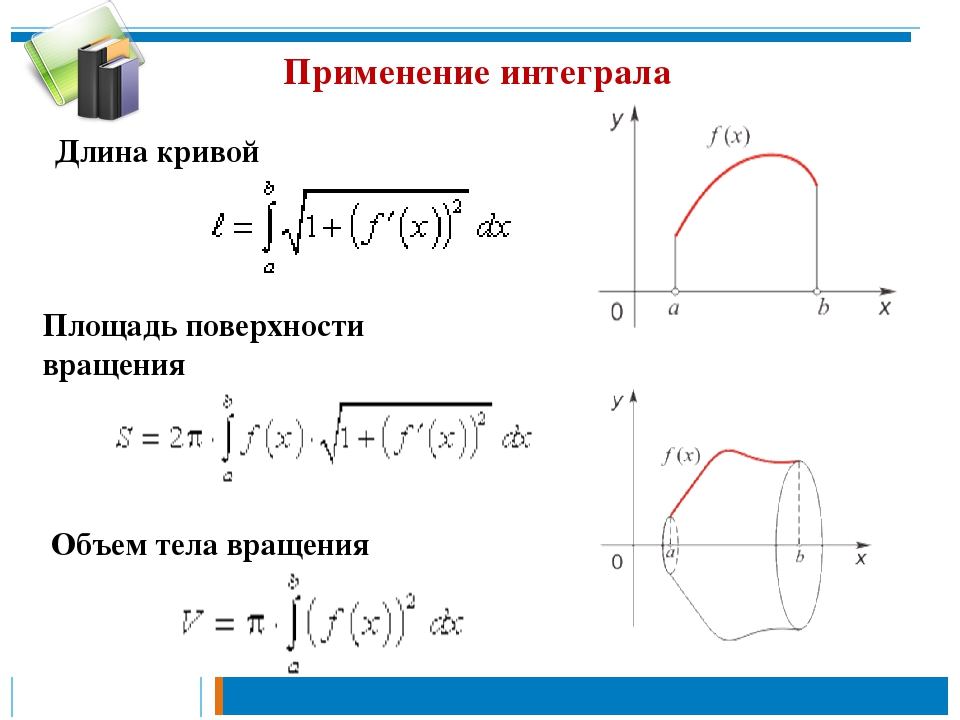
Используйте графическое представление функции для лучшего понимания формы тела.

Нахождение площади поверхности вращения тела

Запомните основные формулы для вычисления площади поверхности тела вращения.

Вычисление площадей и объемов с помощью определённого интеграла

Практикуйтесь в решении задач на вычисление интегралов.
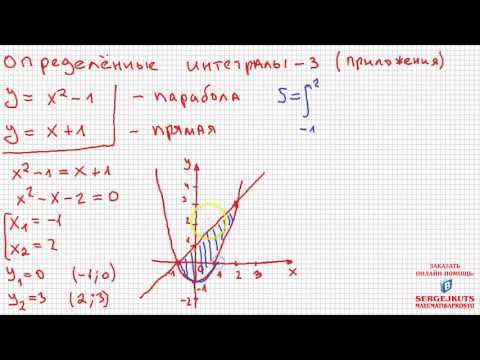
Математика без Ху%!ни. Определенные интегралы, часть 3. Площадь фигуры.
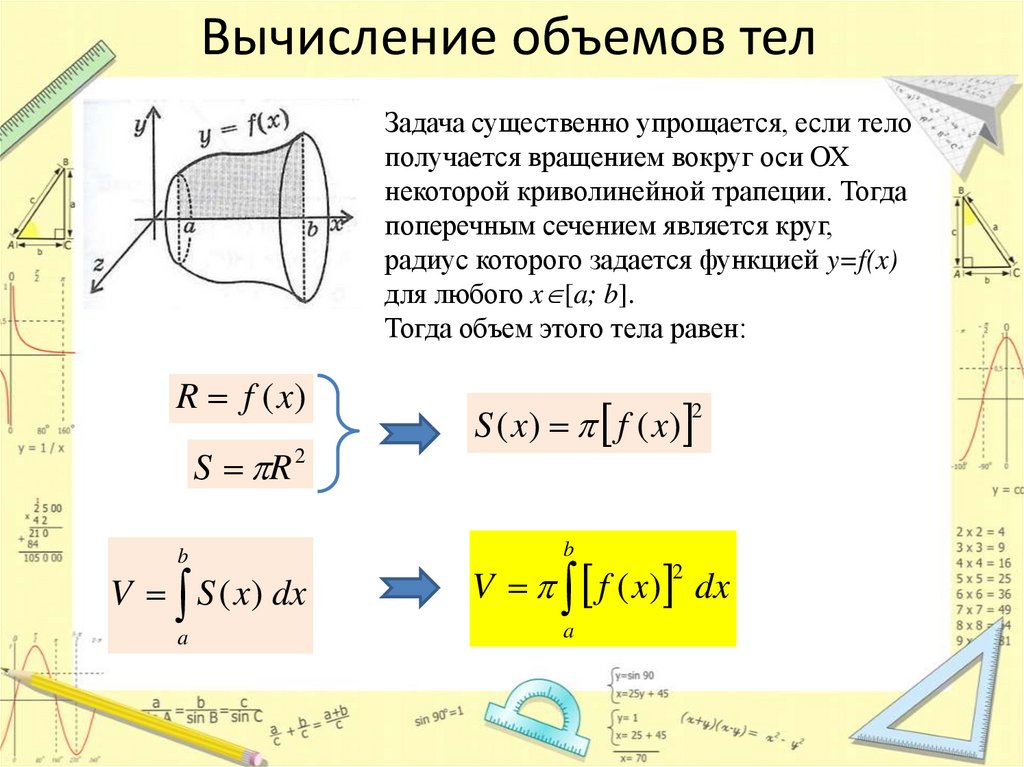
Обратите внимание на точность вычислений, особенно при работе с дробными числами.
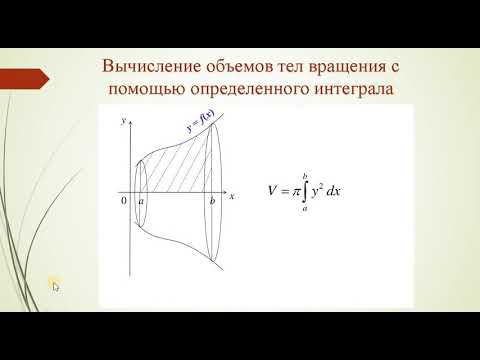
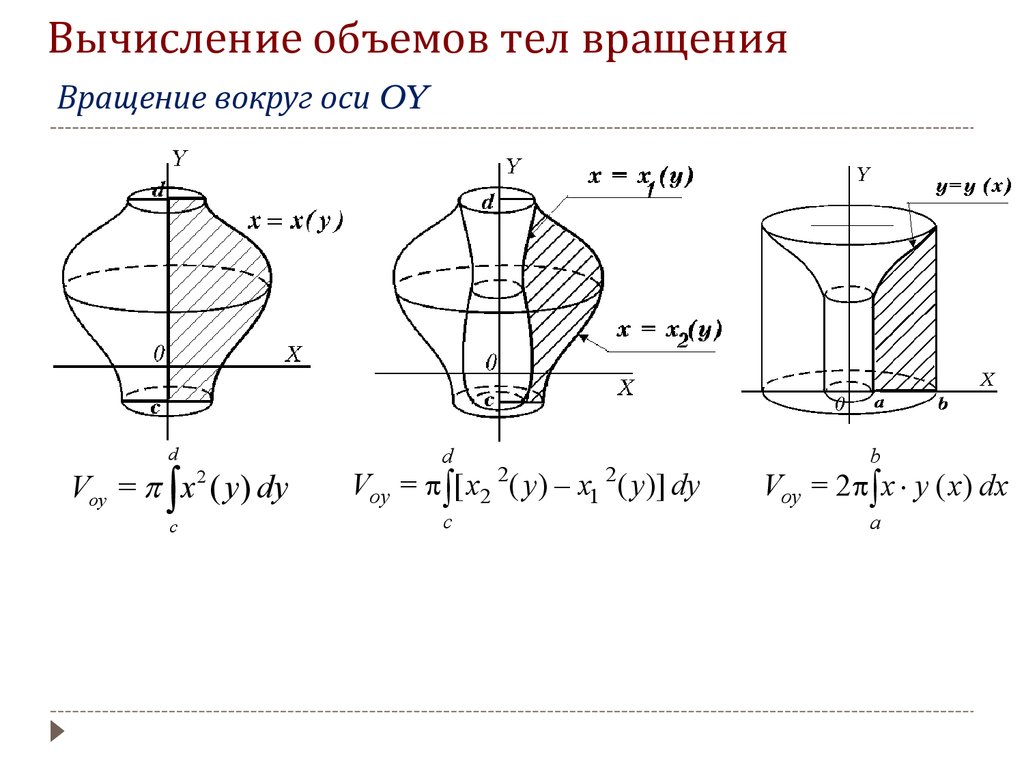
Вычисление объемов тел вращения (применение определенного интеграла)


Изучите применение численных методов для вычисления интегралов.
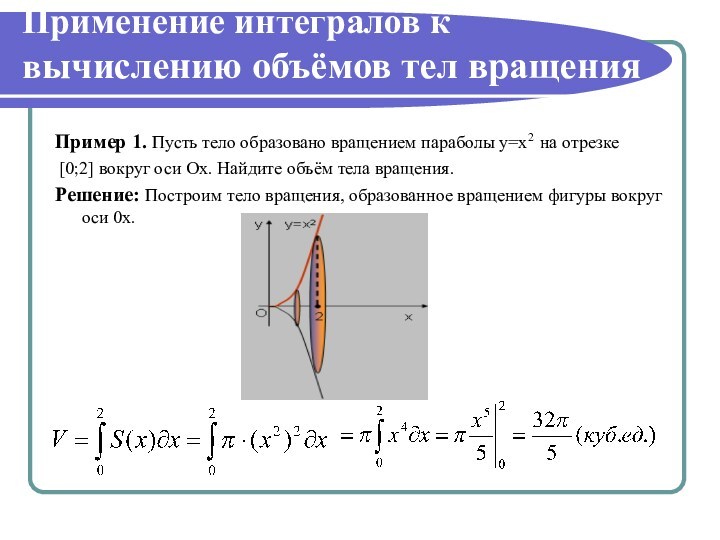
Используйте специализированное программное обеспечение для вычислений.

Помните о важности правильного выбора оси вращения.

1712. Площадь поверхности вращения.


Регулярно проверяйте свои вычисления на наличие ошибок.

Площадь поверхности вращения.

Консультируйтесь с преподавателями или экспертами в случае затруднений.
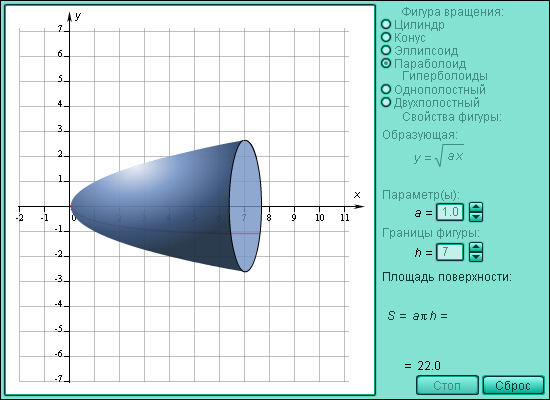

Интегралы №13 Объем тела вращения