Как использовать круги Эйлера и Вена для решения задач в дискретной математике
Круги Эйлера и Вена - мощные инструменты визуализации и анализа, которые помогают в понимании и решении задач в дискретной математике. В этой подборке вы найдете фотографии, иллюстрирующие их применение, а также полезные советы по использованию этих диаграмм в учебе и работе.
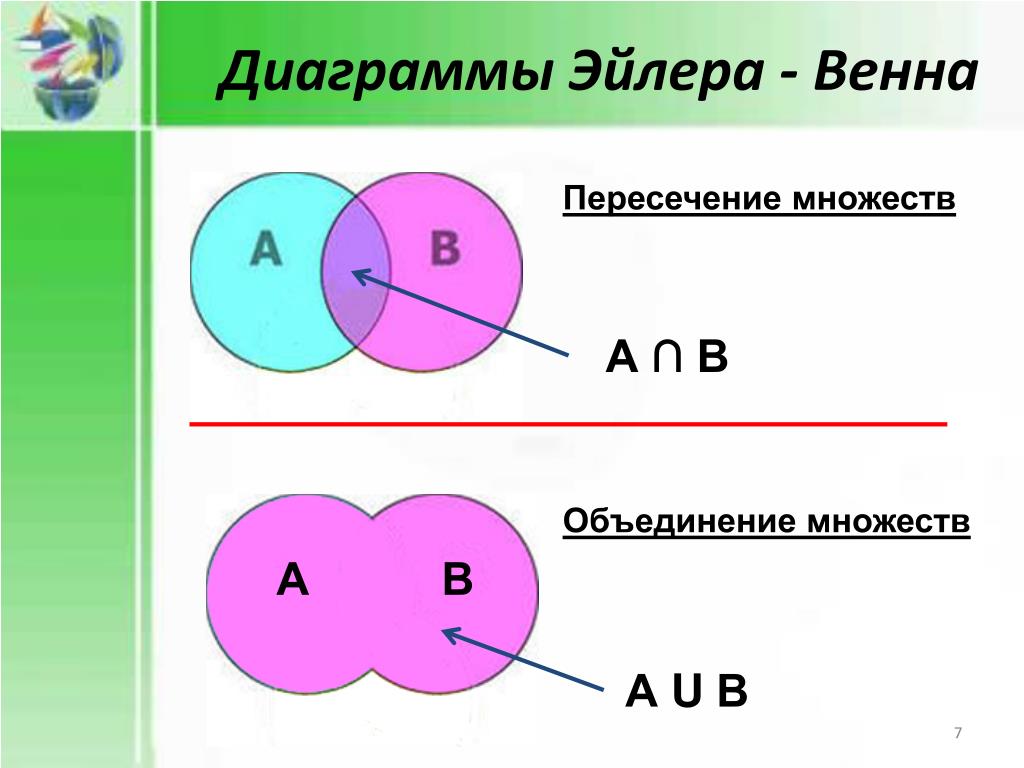
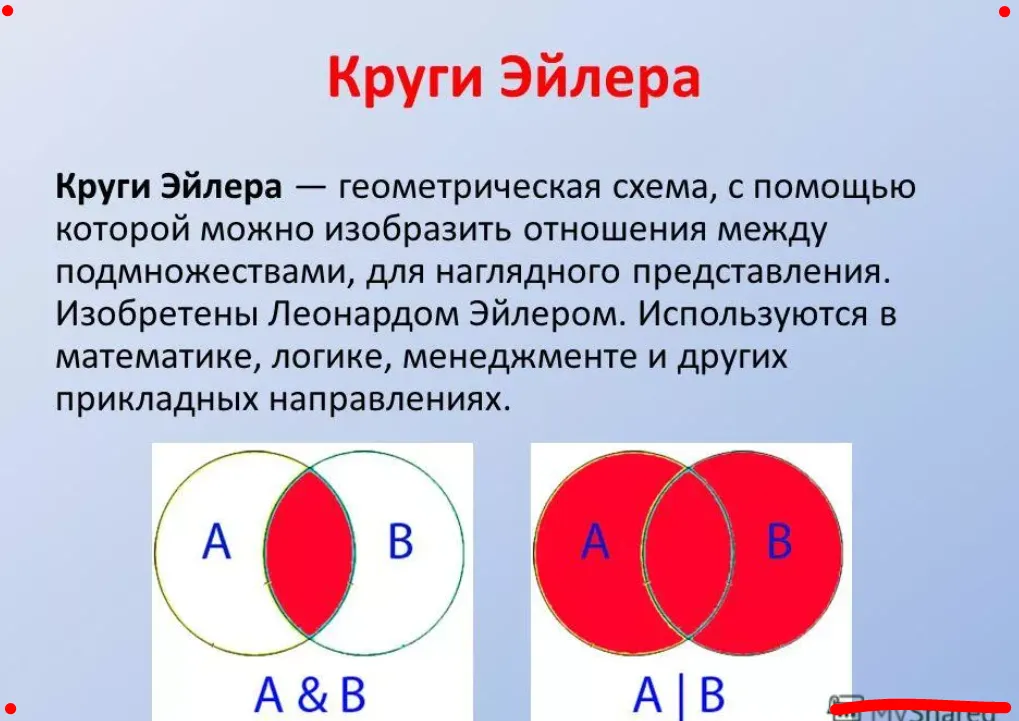
Начните с простых примеров, чтобы понять основы построения кругов Эйлера и Вена.

14. Круги Эйлера
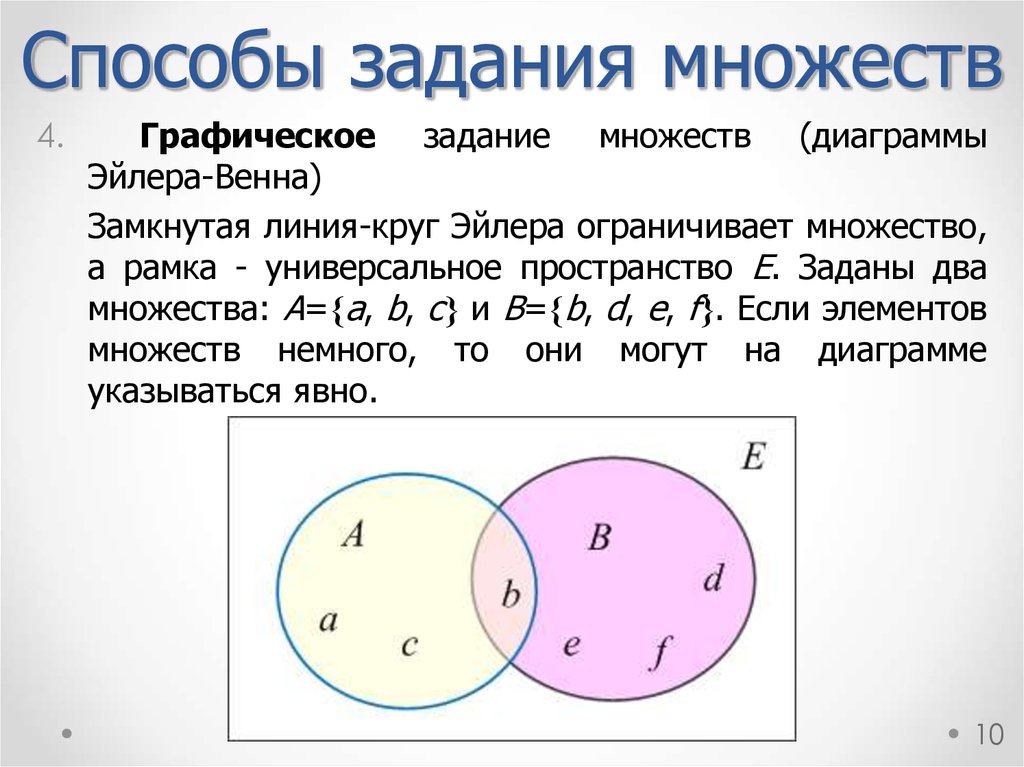

Используйте различные цвета для обозначения пересечений и объединений множеств.

Круги Эйлера. Логическая задача на множества. Иностранные языки
При решении задач на бумаге начертите круги достаточно большими, чтобы было удобно отмечать элементы множеств.

Множества и операции над ними
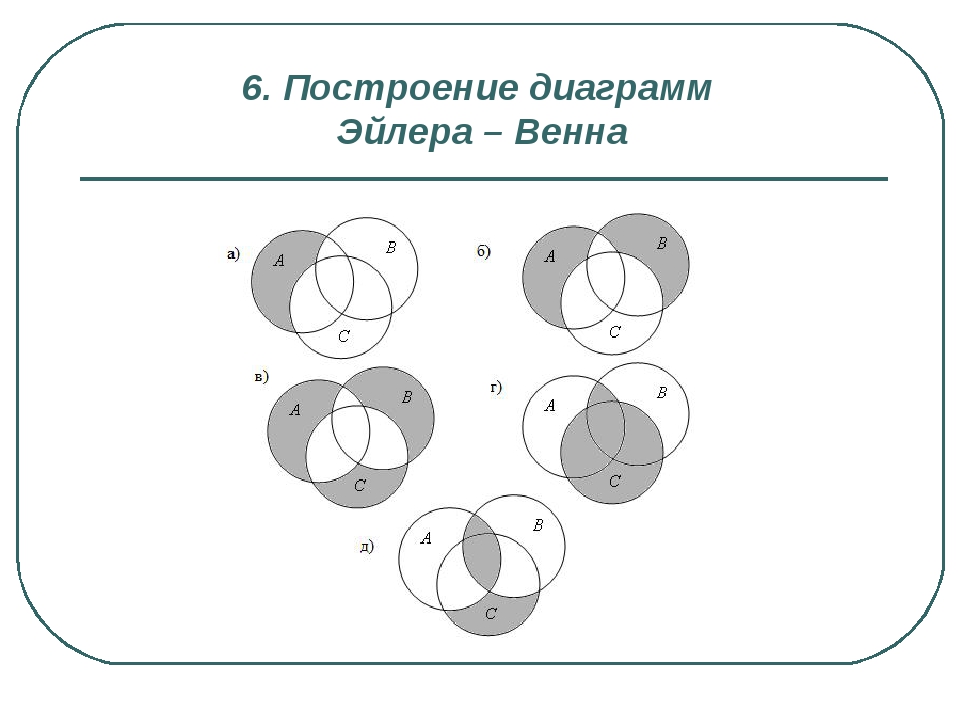
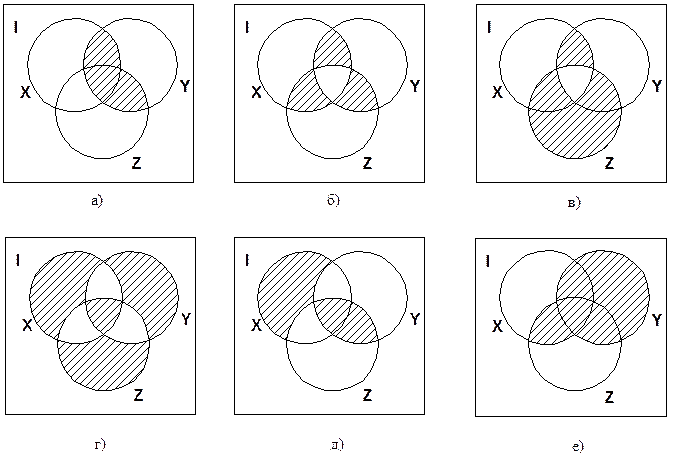
Обратите внимание на правильное расположение кругов для четкого отображения всех возможных пересечений.

Доказать равенства при помощи диаграмм Венна
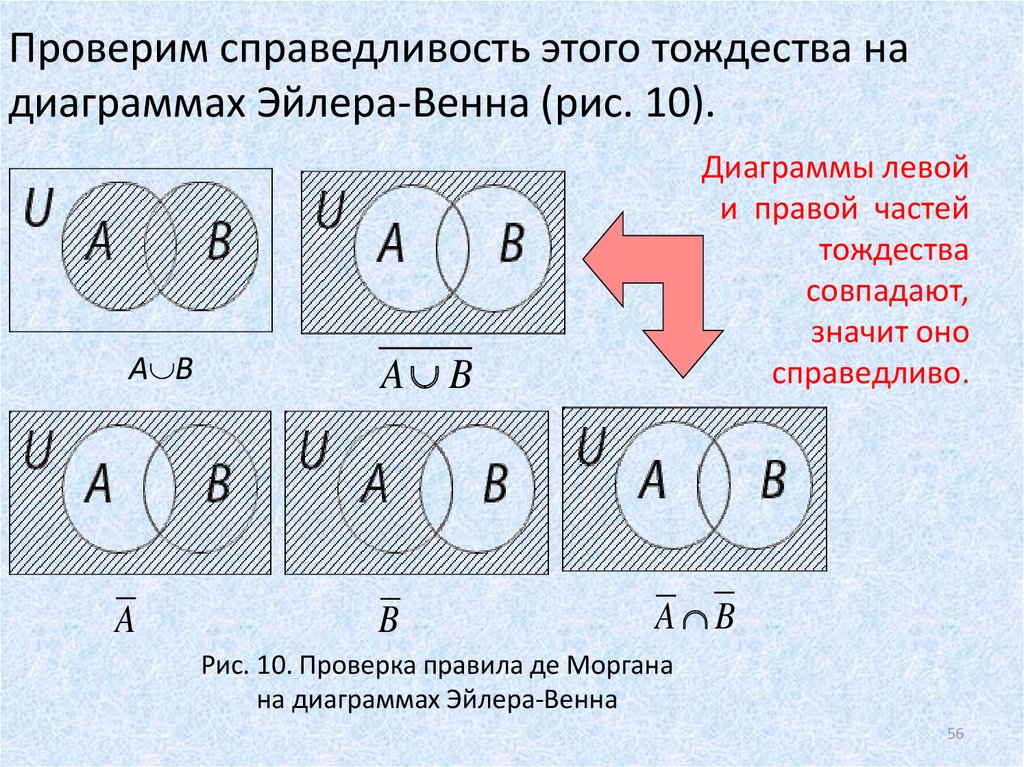
Регулярно практикуйтесь, решая задачи из учебников по дискретной математике.

круги эйлера и логические отношения

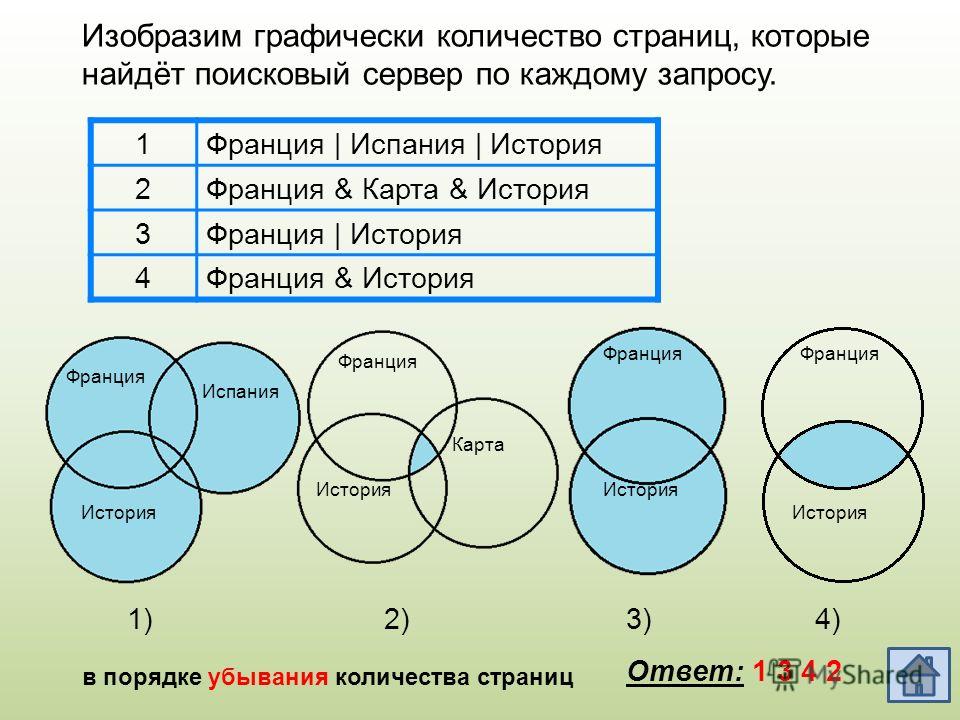
Используйте программные инструменты для создания кругов Эйлера и Вена в цифровом виде.

Доказать равенства при помощи диаграмм Эйлера-Венна. Действия над множествами.

Изучайте примеры применения кругов Эйлера и Вена в различных областях математики и информатики.
Постарайтесь находить взаимосвязи между множествами для более глубокого понимания задач.

Круги Эйлера и их применение в текстовых задачах.
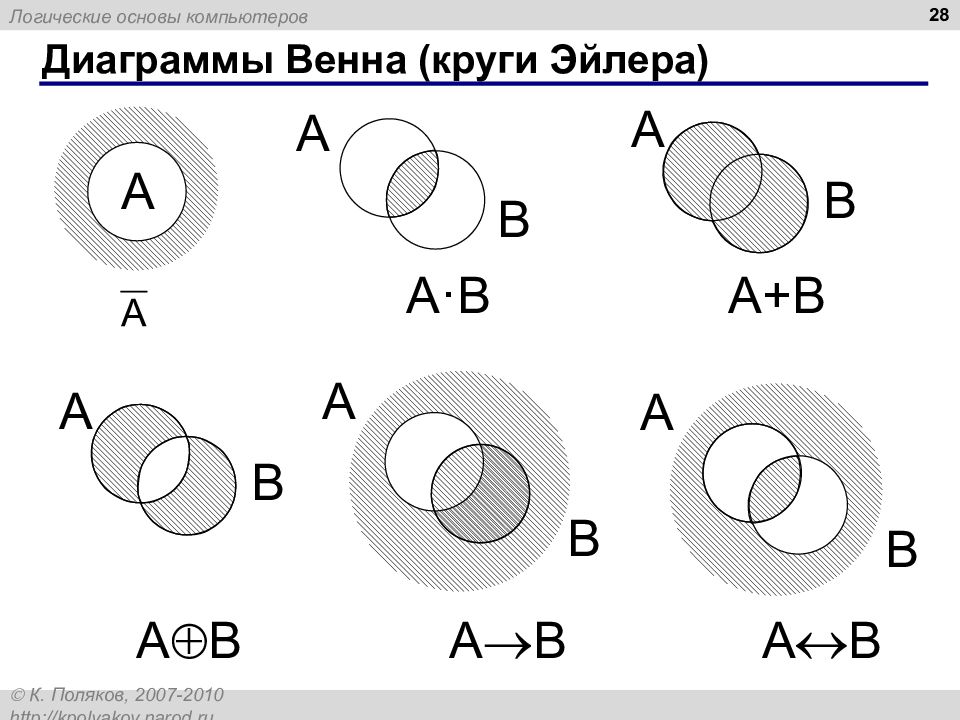
Не бойтесь экспериментировать с различными подходами к построению кругов.
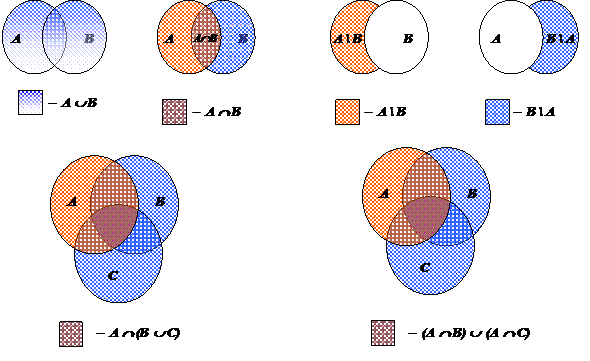
Используйте круги Эйлера и Вена для визуализации сложных логических задач и отношений между множествами.