Понимание канонических видов кривых и поверхностей в математике
Канонический вид кривых и поверхностей — это важная тема в математике, особенно в области аналитической геометрии и дифференциальной геометрии. Он помогает упростить уравнения кривых и поверхностей, делая их анализ и работу с ними более удобными. В данной статье мы рассмотрим основные типы кривых и поверхностей, их канонические формы и примеры применения.


Изучите основные типы кривых и поверхностей, такие как окружности, эллипсы, гиперболоиды и параболические цилиндры, чтобы лучше понимать их канонические виды.

Приведение поверхности второго порядка к каноническому виду ортогональным преобразованием.


Практикуйтесь в преобразовании уравнений кривых и поверхностей в их каноническую форму, чтобы облегчить решение задач и упрощение расчетов.

Ошибки КР \

Используйте графические программы для визуализации кривых и поверхностей, чтобы лучше усвоить их свойства и формы в каноническом виде.
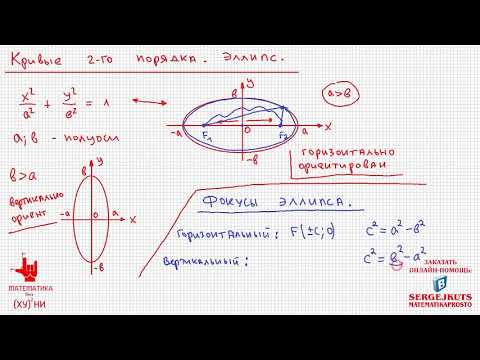
Математика без Ху%!ни. Кривые второго порядка. Эллипс.


Обратите внимание на связь между каноническим видом и другими математическими концепциями, такими как собственные векторы и значения, чтобы получить более глубокое понимание темы.

Кривые второго порядка. Эллипс. Приведение к каноническому виду и чертеж
Практикуйтесь на примерах из реальных задач, чтобы увидеть, как канонический вид применяется на практике в различных областях науки и техники.

Метод Лагранжа. Приведение квадратичной формы к каноническому и нормальному видам

Разберитесь в методах диагонализации матриц, так как они часто используются для приведения уравнений до канонического вида.

Обратите внимание на преобразования координат, которые могут помочь в нахождении канонического вида для более сложных кривых и поверхностей.

Самый короткий тест на интеллект Задача Массачусетского профессора

Чтение специализированной литературы и учебников по дифференциальной геометрии может помочь углубить знания о канонических видах и их применении.

Канонический вид кривой второго порядка

Регулярно решайте задачи по аналитической геометрии, чтобы поддерживать и улучшать навыки работы с каноническими видами кривых и поверхностей.


Посещайте семинары и вебинары по математике и геометрии, чтобы быть в курсе новых методов и подходов в анализе кривых и поверхностей.
