Понимание рациональных чисел: определение и примеры
Рациональные числа — это числа, которые можно представить в виде дроби, где числитель и знаменатель являются целыми числами, и знаменатель не равен нулю. Они включают в себя все целые числа, дроби и конечные десятичные дроби. Рациональные числа важны в математике и используются во многих реальных приложениях.



Рациональные числа включают как положительные, так и отрицательные дроби.

Натуральные числа, целые числа, рациональные числа, иррациональные числа и действительные числа

Любое целое число можно представить в виде дроби, добавив знаменатель 1.

Рациональные и иррациональные числа за 5 минут

Для сравнения рациональных чисел можно привести их к общему знаменателю.

Математика 6 класс - рациональные числа и действия над ними. Перевод обыкновенной дроби в десятичную
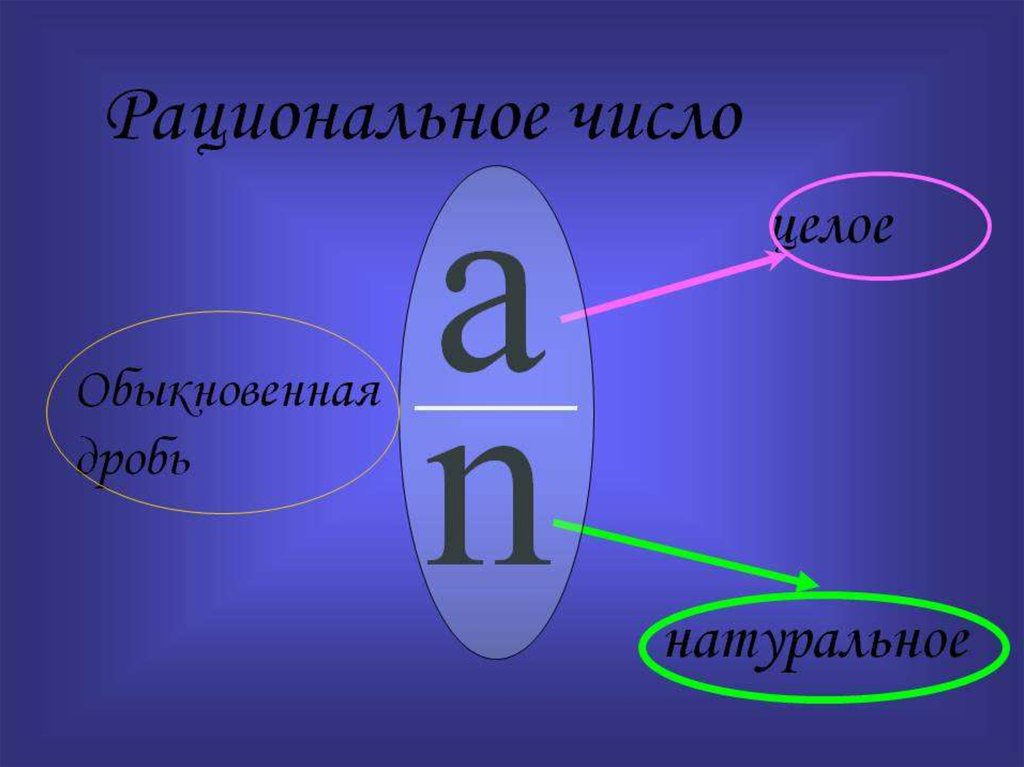
Рациональные числа могут быть конечными или периодическими десятичными дробями.

Какие числа называются рациональными
При делении двух целых чисел всегда получается рациональное число.

Какие числа называются рациональными. Математика. 6 класс.


Сложение и вычитание рациональных чисел требует приведения дробей к общему знаменателю.

Всё про рациональные числа за 10 минут - Осторожно, спойлер! - Борис Трушин -
Умножение рациональных чисел осуществляется путём перемножения числителей и знаменателей.

1 . Рациональные числа (Макарычев, 7 класс)

Деление рациональных чисел сводится к умножению на обратную дробь.

Урок по теме РАЦИОНАЛЬНЫЕ ЧИСЛА.


Для рациональных чисел характерно свойство плотности: между любыми двумя рациональными числами можно найти ещё одно рациональное число.
Целые и рациональные числа. 6 класс.
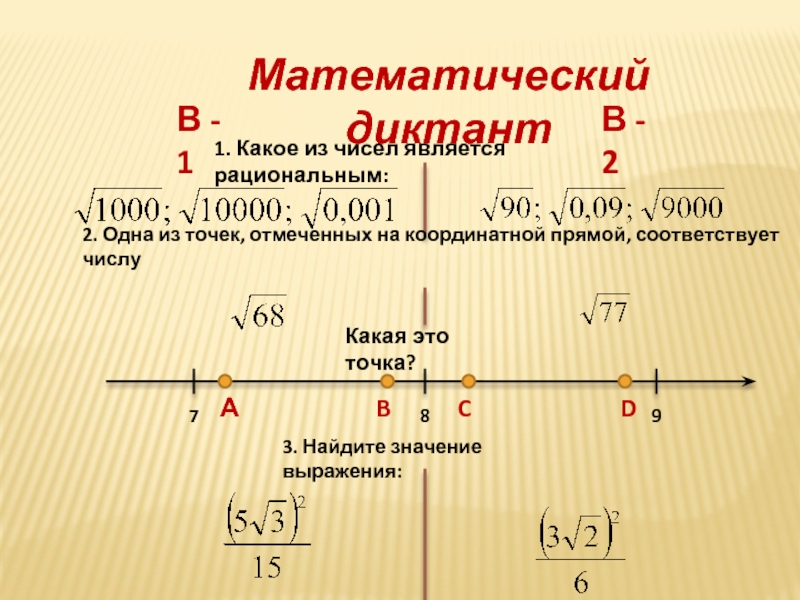

Рациональные числа часто используются для измерений и расчётов в реальной жизни, таких как финансовые операции и технические вычисления.