Как правильно вычислять интегралы с комплексными переменными: советы и рекомендации
На этой странице представлены полезные советы и пошаговые инструкции по вычислению интегралов, содержащих комплексные переменные. Эти интегралы часто встречаются в различных областях математики и физики, и правильное их вычисление требует понимания определенных методик и приемов. Мы расскажем о ключевых аспектах и предложим практические рекомендации для более эффективного решения задач.


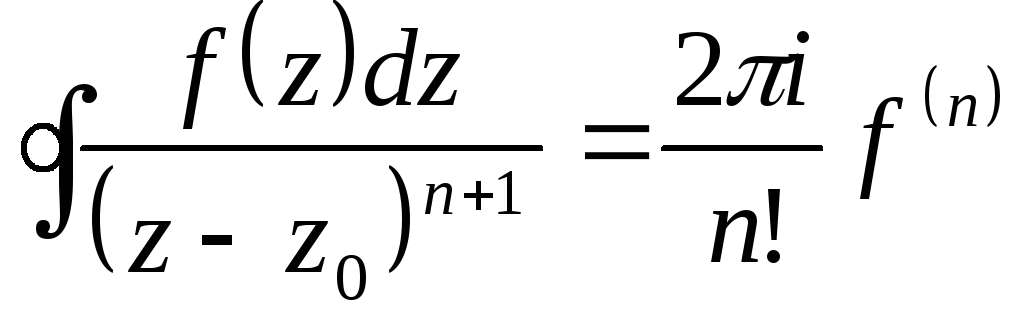
Обратите внимание на область интегрирования: правильно определите границы интеграла.
Complex Integration and Finding Zeros of the Zeta Function
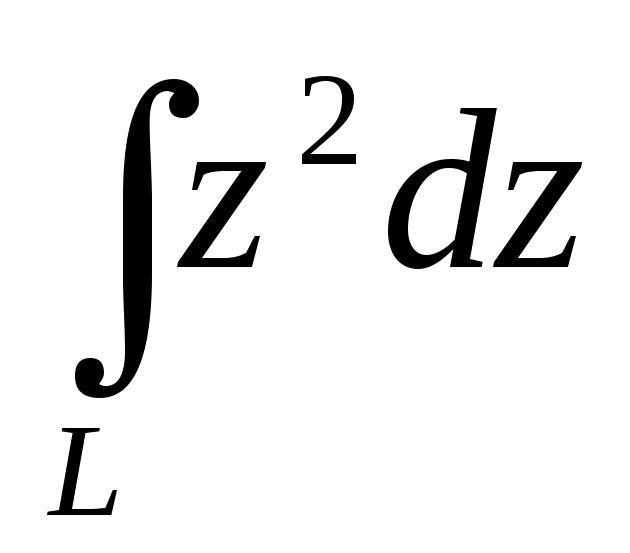
Используйте свойства комплексных функций для упрощения вычислений.

Evaluate the integral 𝐼=∫𑀾 𝑅𝑒𝑧 𝑑𝑧 , on the circle -𝑧-=𝑟 .

При решении интегралов с комплексными переменными полезно применять метод резидуума.

Evaluate the integral ∫𑀾 𝑧̅ 𝑑𝑧 where 𝐶 is the straight line from the point (1,0) to the point (1,1)
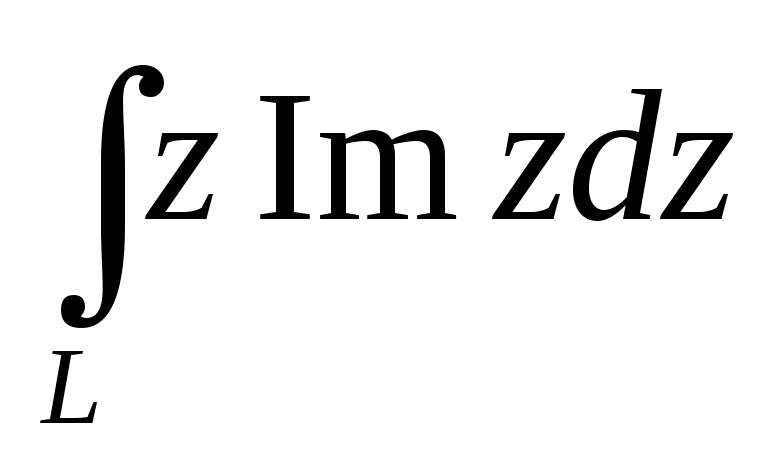
Рассмотрите возможность использования замен переменных для упрощения интеграла.

Calculus Help: Integral of Complex Analysis: Integral of z conjugate where C: -z-=2 ∫C z ̅ dz
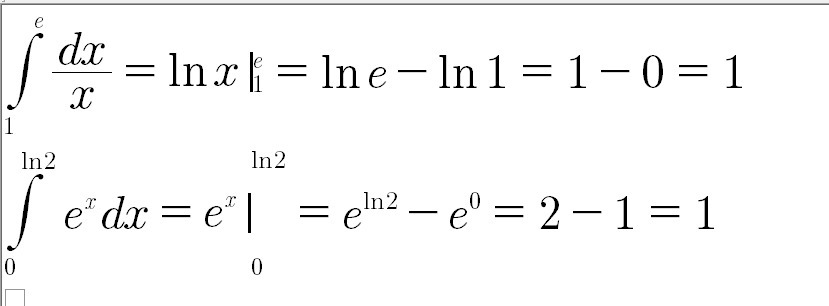
Помните о правилах вычисления интегралов по контуру в комплексной плоскости.

Evaluate integrate z^2 from 0 to 1+i w. r. t. z.
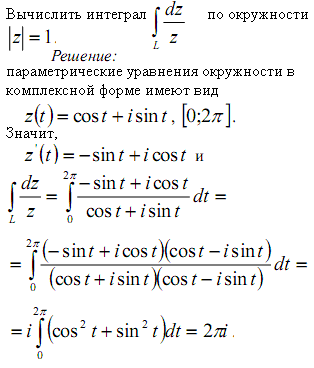

Проверяйте свои вычисления на наличие ошибок и согласованность с теорией.
Используйте специализированное программное обеспечение для проверки и упрощения интегралов.

Evaluate ∫𑀾 𝑧̅ 𝑑𝑧 , from 𝑧 = 0 to 𝑧 = 4+2𝑖 along the curve 𝐶 given by 𝑧 = 𝑡² + 𝑖𝑡 .
Решайте задачи в несколько этапов, чтобы избежать ошибок при вычислениях.
Сравните свои результаты с известными примерами и стандартными решениями.

Evaluate ∫𑀾 𝑧𝑑𝑧 .

Практикуйтесь регулярно, чтобы улучшать навыки работы с интегралами комплексных функций.
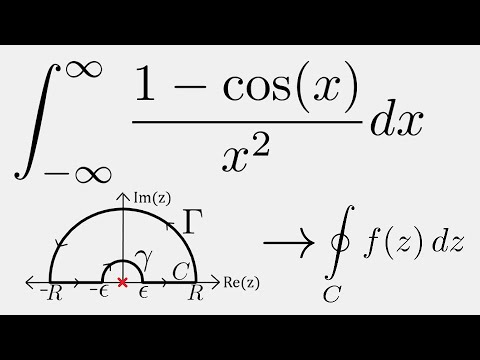
Complex Analysis: Integral of (1-cos(x))/x^2 using Contour Integration


Evaluate the following complex path integral I = Jc Rez dz C the shortest path from 1+ i to 3 + 3i