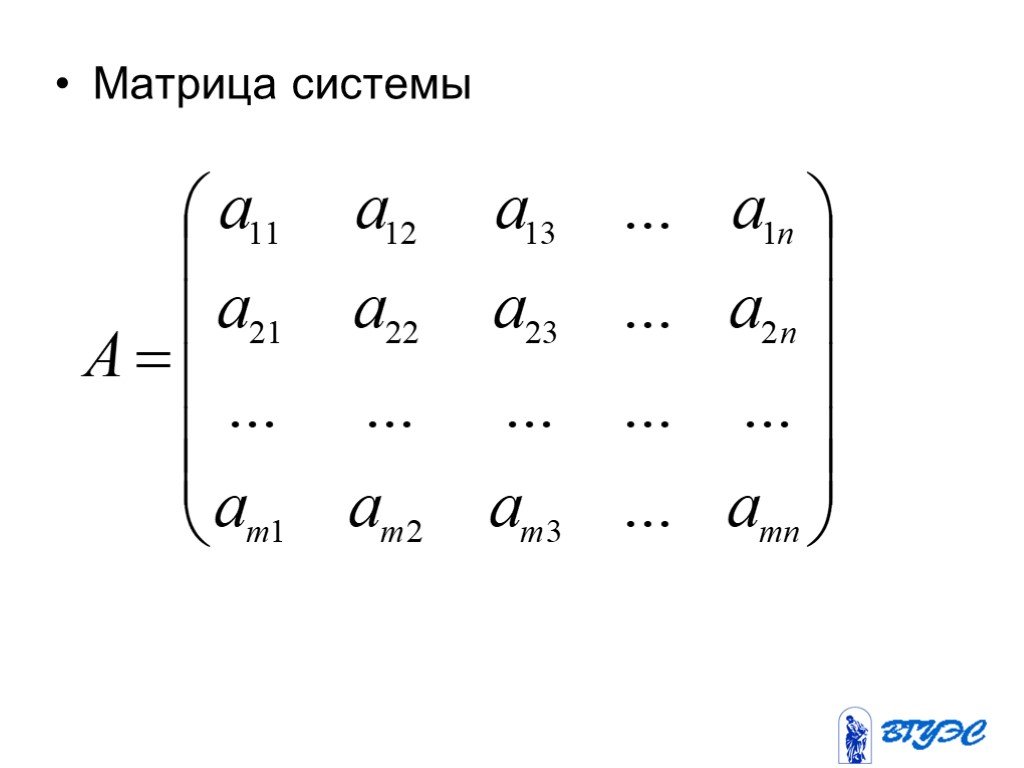
Как использовать главную матрицу для решения систем линейных уравнений
Главная матрица является важным элементом при решении систем линейных уравнений. В этом разделе мы рассмотрим основные методы и советы по ее использованию.



Проверьте правильность составления матрицы, чтобы избежать ошибок в вычислениях.

Линейная алгебра, Матрицы: Метод Гаусса. Высшая математика

Используйте методы Гаусса или Гаусса-Жордана для упрощения матрицы.

Система линейных уравнений. Метод обратной матрицы. Матричный метод.

Убедитесь, что все коэффициенты правильно занесены в матрицу перед началом расчетов.

Общее, частное, базисное решение системы линейных уравнений Метод Гаусса

При наличии нулевых строк в матрице проверьте систему на совместимость.

Решение системы уравнений методом Гаусса
Используйте программное обеспечение для автоматизации расчетов с матрицами.

Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvy

Проверьте, чтобы все элементы главной диагонали были ненулевыми, если это возможно.

Применяйте обратную матрицу для решения системы, если она существует.
Математика машинного обучения/Анализ данных/Теория вероятностей/Статистика/Линейная алгебра/Матан
Используйте определители для проверки существования и единственности решений.

Разбивайте сложные системы на более простые подзадачи для упрощения расчетов.

Изучите теорию линейной алгебры для более глубокого понимания работы с матрицами.

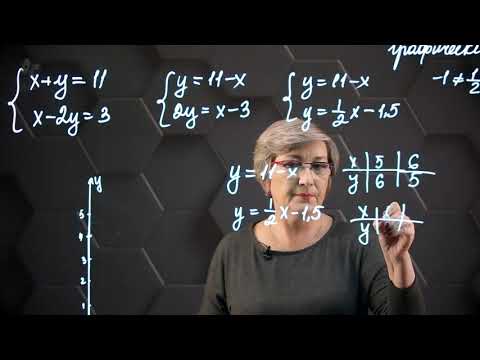
Решение системы линейных уравнений графическим методом. 7 класс.